ЧЕРНОВИК

ДИССЕРТАЦИИ

13.00.02 - теория и методика обучения и воспитания
(информатизация образования, информатика)

диссертация на соискание ученой степени
кандидата педагогических наук

Пантуева Андрея Валерьевича

Методические проблемы построения элективного курса-практикума по математическому моделированию для профильных классов в среде Geometer's SketchPad.

Москва - 2004

Работа выполнена на кафедре информатики Московского Городского Педагогического университета.

Научный руководитель:

доктор педагогических наук, профессор А.С.Лесневский

Официальные оппоненты:

доктор физико-математических наук, профессор Н.Х.Розов (МГУ)
кандидат педагогических наук, доцент С.В.Бирюков (МПГУ)

Механика.

Построение моделей шарнирных механизмов и анализ траекторий.

Механическое моделирование в работах П.Л.Чебышева

С именем замечательного русского математика 19-го столетия Пафнутия Львовича Чебышева связаны приложения математики к механике. Интересно, что Пафнутий Львович сам вытачивал на станках свои шарнирные механизмы, в основном из бронзы. В Санкт-Петербурге, в музее истории науки до сих пор хранится шкаф с его моделями.

Механика была источником постановки математических задач, блестяще решенных Чебышевым. В частности, знаменитые многочлены Чебышева возникли при решения задач механики.( Артоболевский И. И., Механизмы в современной технике, т, 1-2, М., 1970-71.)

Так, классическая теория наилучших приближений функций возникла в процессе усовершенствования П. Л. Чебышевым параллелограмма Уатта в паровой машине.

Помимо параллелограмма Уатта, Чебышев интересовался и другими шарнирными механизмами, о чем свидетельствуют, например, такие его работы, как «О некотором видоизменении коленчатого параллелограмма Уатта» (1861), «О параллелограммах» (1869), «О параллелограммах, состоящих из трех каких-либо элементов» (1879) и др. Он сам занимался конструированием механизмов, построил знаменитую «стопоходящую машину», воспроизводящую движение животного при ходьбе, автоматический арифмометр, механизмы с остановками и множество других механизмов.

Шарнирные механизмы и их математические модели.

Шарнир - сочленение стержней, оставляющее им возможность ограниченного движения. Самый простой шарнир - общая ось двух стержней. Немного более сложный шарнир - штанга, и т.д.

Мы рассмотрим модели следующих механизмов:

Витгенштейна
для построения параболы
Уатта
Чебышева (ШРМ «с задержками»

Механизм Витгенштейна

Определение механизма Витгенштейна

Этот пример неожиданно разнообразных и сложных форм кривых, получающихся при работе простейших механизмов, дан выдающимся лингвистом и философом первой половины XX века Людвигом Витгенштейном.

Механизм описывается так: дан стержень фиксированной длины, проходящий через данную точку. Например, он продет в кольцо, которое закреплено на плоскости, но может так вращаться, чтобы стержень беспрепятственно и поворачивался в нем, и скользил внутри него.

Вопрос: если один конец этого стержня скользит по окружности, то какую траекторию может описывать второй его конец?

Как показать конструкцию, не давая при этом подсказки.

Методический прием, который мы применяем при пояснении конструкции механизма, таков - мы показываем движение построенного механизма, но при этом на таком коротком отрезке траектории, чтобы это не было подсказкой, а было только пояснением именно к конструкции.

Наиболее частая ошибка учащихся - предполагать, что движение второго конца стержня также будет совершаться по окружности, поэтому пример движения не должен противоречить этому ложному предположению - в его ложности учащиеся должны убедиться сами, на построенной самостоятельно конструкции.

Построение учащимися модели механизма.

Напоминание о способе построения засечки.

При построении важно понять, что дано по условию, что может изменяться, и что требуется найти. Для класса, хорошо успевающего по геометрии, это не составляет никаких проблем.

Сильные учащиеся сразу строят правильный чертеж, как только они вспоминают о команде «построить окружность из данной точки по данному радиусу, заданному отрезком». Эту команду можно напомнить всем, как обычное средство построения засечек на чертеже.

Алгоритм построения модели.

Начертим окружность инструментом «циркуль». Поставим инструментом «точка» две точки - одну вне окружности, другую точно на окружности. Инструментом «отрезок» начертим в углу чертежа отрезок, который будет задавать длину стержня. Из точки, построенной на окружности, проведем луч через точку, построенную вне окружности. На луче от вершины отложим отрезок, равный заданному - это делается с помощью построения засечки на луче. Иначе говоря, нужно выделить вершину луча и построенный отрезок (в углу чертежа), и выполнить команду «окружность по центру и радиусу» из меню «Построение». После чего от точки пересечения до вершины луча построить отрезок (не смущаясь, что он лежит на луче), а луч и вспомогательную окружность спрятать (а не удалить!). Задав свойство точке конца отрезка «оставлять след» (команда «оставлять след» меню «вид», или через контекстное меню, вызываемое правой кнопкой мыши), и задав цвета и жирность точкам, отрезку и окружности , можно приступать к экспериментам.

Ход построения модели механизма Витгенштейна.

Пояснение. (Рисунок 1.) Вершина луча - на окружности. Луч проходит через фиксированную точку на плоскости.( Рисунок 2.) Откладываем на луче данный отрезок, делая засечку на нем. (Рисунок 3.) Луч спрятан. Построена модель стержня данной длины, проходящего через данную точку, один конец которого скользит по окружности.

Эксперименты с моделью: след и живой след.

Двигая точку, изображающую конец стержня, по окружности, учащиеся обнаруживают, что траектория сложнее, чем они предполагали. Они обнаруживают, что траектория симметрична и непрерывна. Изменив длину стержня или взаимное расположение исходных точек, они получают различные кривые. На этом этапе совершенствования модели можно остановится, и создать коллекцию кривых.

Для этого достаточно сохранять каждую из избранных таким образом кривых в графическом формате (это или WMF, или EMF), или делать скриншоты экрана.

Из полученных файлов можно сделать или альбом, или документ WORD, или любую другую форму презентации, которой владеют ученики, в том числе и многостраничный чертеж Живой Геометрии.

Коллекция скриншотов следа для механизма Витгенштейна при различных его параметрах - длине стержня, радиуса окружности и положении «гвоздя».

Но есть и более мощный метод исследования такого рода чертежей. Там, где нужно изучать конфигурацию следа точки, или отрезка, или окружности, или дуги и т.д., целесообразно построить новый динамический объект - «геометрическое место точек, отрезков, окружностей, дуг и т.д., при всех возможных положениях точки-параметра».

Строится он просто - выделяется объект, чей след изучается, и выделяется точка-параметр. После этого выполняется команда «Геометрическое место точек» (locus, или, в одной из версий, «Живой след») из меню Преобразования.

Теперь при изменении параметров чертежа новый объект-след будет также непрерывно (непрерывность, здесь, конечно, компьютерная и заметно зависит от быстродействия компьютера и заданного количества точек-звеньев) меняться. Этот объект тоже может, в свою очередь, оставлять следы, но образовать от него, в свою очередь, «живой след» среда не позволяет.

Рисунки показывают, как изменяетс я «живой след» при плавном уменьшении длины стержня и как - при плавном увеличеснии радиуса окружности в модели Витгенштейна.

Механизм, строящий параболу.

Явное геометрическое определение параболы.

Простой, но полезной и эффектной моделью шарнирного механизма является модель механизма, реализующего параболу. Из множества таких механизмов мы выбрали тот, который ближе всего к школьному курсу.

Задача формулируется так: построить след пересечения серединного перпендикуляра к отрезку, один конец которого движется по оси абсцисс, и перпендикуляра к оси абсцисс из этой же точки. Второй конец отрезка закреплен на оси ординат.

Неявное геометрическое определение параболы

Эта задача получается из другого, неявного определения кривой:

построить геометрическое место точек, равноудаленных от данной прямой и данной точки.

По неявному определению можно построить кривую методом проб и ошибок, подбирая точки, удовлетворяющие ему.

Это действие, сходное с решением уравнения методом подбора, близко к применению методики «черного ящика». Действительно, предлагая выбранную точку, мы должны для нее произвести заданную процедуру - измерить и сравнить некоторые расстояния, и тогда только получить ответ, характеризующий точку - принадлежит она кривой или нет.

Лабораторная установка для экспериментальной работы.

Она вычисляет нужные расстояния для точки, которую мы можем перемещать курсором, и при малой разнице между этими расстояниями включает свойство точки оставлять след на чертеже.

Таким образом, перемещая курсор по чертежу, мы можем обнаруживать точки, удовлетворяющие неявному определению. Для учащихся ставится задача - обнаружить как можно больше таких точек на своем чертеже.

Об уровне сложности «экспериментальной установки».

Лабораторную работу можно делать на готовой «установке», а можно и построить её прямо на уроке. Построение, конечно, предпочтительнее, но при малости времени или других ограничениях приходится пользоваться готовыми моделями.

Когда и какие модели строить, а когда использовать готовые - зависит от оценки эффективности работы по построению модели как элемента курса информатики. В частности, и от такой характеристики модели, как её сложность.

Для данной модели, как и для большинства представленных моделей, можно выбрать или более простой, или более универсальный вариант, соответственно алгоритм реализации будет проще или сложнее.

Самый простой вариант - на чертеже с двумя уравниваемыми расстояниями от «пробной» точки приготовить десятка два-три кружочков (копированием одного кружка), и расставлять их в тех точках, где расстояния уравнялись.

Более сложный для построения, но более удобный в работе вариант - когда эта работа по расставлению кружочков автоматизируется - «пробный кружок» сам оставляет свой след на чертеже, если расстояния становятся очень близки.

В построении такой модели используется следующее свойство среды моделирования. Если объекты пересекаются, то точка пересечения может быть исходной для каких-то построений, например для отрезка. Но если в процессе перемещения каких-то элементов чертежа (например, мышкой двигаем какую-то точку) отрезки перестанут пересекаться, исчезнут с чертежа и точка пересечения, и все конструкции, построенные с ее помощью.

Так, лабораторная установка строится при помощи построения маленькой окружности вокруг двигаемой точки, существование которой зависит от разности между уравниваемыми расстояниями.

Работа на экспериментальной установке по изучению геометрического места точек, заданного равенством.

Пояснение. Модель построена так, что при малой разности уравниваемых расстояний передвигаемая мышкой точка начинает оставлять след, и оставляет его до тех пор, пока разность расстояний не увеличиться. Таким образом мы делаем видимым геометрическое место точек (конечно, приближенно, так как малая разность - все же не нулевая)

Лабораторная установка по работе с явным определением.

От экспериментальных результатов можно теперь перейти к получению явного определения кривой. При этом качество и трудоемкость построения кривой по явному определению будут настолько лучше этих результатов, что работа по получению явного определения приобретает дополнительный смысл и мотивацию.

Явное определение связано с известным свойством равнобедренного треугольника, в котором высота к основанию является и медианой. Используя это свойство, можно доказать, что для нахождения всех точек параболы необходимо и достаточно найти все точки пересечения двух перпендикуляров: серединного перпендикуляра к отрезку, один конец которого движется по оси абсцисс, и перпендикуляра к оси абсцисс из этой же точки.

Переход к алгебраической (функциональной) характеризации кривой.

Если теперь рассмотреть соответствующие геометрические закономерности, задающие этот механизм, выписать их и выбрать простейшие единицы измерения (т.е. применить простейшее «обезразмеривание»), то можно сделать следующий шаг.

Получение уравнения кривой, заданной геометрически.

Пояснение. Динамический чертеж помогает выделить и выписать закономерности в алгебраической форме. Например, подобие треугольников хорошо заметно при движении, изменяющем углы на чертеже. Все получаемые формулы можно проверять измерениями - для контроля (на рисунке не показаны).

Теперь можно построить график кривой на том же чертеже, и проверить их совпадение прямым наложением. Если нет ошибок, кривые совпадут.

Проверка совпадения геометрического и алгебраического определения кривой.

Пояснение. Проверка состоит в построении на одном чертеже двух кривых. Одна построена как след некоторой точки, а другая - как график функции. При выборе правильного масштаба их можно непосредственно наложить друг на друга, и визуально убедиться в их совпадении.

Построение кривых учащимися по своим собственным алгоритмам.

После выполнения этой работы можно перейти к заданию построения собственных механических кривых. Требования к ним минимальны - это не должна быть окружность, механизм должен быть не слишком сложен, и использовать только построения циркулем и линейкой. Конечно, алгоритм построения должен быть кратко, но ясно описан по шагам.

Приведем примеры выполнения учащимися этого задания.

Построение Сергея Грибовского.

Алгоритм построения (циркулем и линейкой) механической кривой Сергея Грибовского (10в СУНЦ 2004/2005)

Построим окружность (на рисунке - малую) данного радиуса R1 с центром в данной точке B.
На окружности построим точку G.
Построим окружность (на рисунке - большую) по двум точкам - по точке G как центру и по данной точке С, через которую окружность должна пройти.
Отметим на прямой, соединяющей точки G и B, точку Е - точку пересечения с «большой» окружностью.
Построим точку F как середину отрезка EG.
Зададим кривую как геометрическое место точек F при движении точки G по «малой» окружности.

Алгоритм построения кривой, его геометрическое описание и модель.

Пояснение. Прямое построение геометрического места точек для фигуры, придуманной Сергеем Грибовским. На чертеже измерены величины, параметризующие полученную фигуру. Сергей выбрал их из интуитивных геометрических соображений. Теперь ему нужно получить уравнение построенной кривой.

Сергей решил строить уравнение своей кривой в полярной системе координат, и выбрал

три параметра, исчерпывающе характеризующие кривую - радиус малой окружности и полярные координаты точки С (центр системы координат он взял в точке В).

Получение уравнения по геометрическому описанию механизма. Работа Сергея Грибовского, 10в, СУНЦ МГУ, 2005

Пояснение. После вычислений формула, задающая радиус точки кривой в полярных координатах в зависимости от угла, была получена, и по ней построен график.

Он оказался похож на график механической кривой.

Уравнение своей кривой Сергей вывел в полярной системе координат, выбрав

Проверка наложением совпадения геометрической (механическая кривая) и алгебраической (график функции) моделей.

Он оказался похож на график механической кривой. Для более точной проверки обе кривые были построены на одном графике, на основе одних и тех же параметров.

Для экспериментальной проверки совпадения кривых они накладываются друг на друга.

После этого производится вариация параметров, и совпадение должно сохраняться при любых сочетаниях их значений (конечно, в пределах ОДЗ). Конечно, экспериментальная проверка - не доказательство, но все же это аргумент в пользу правильности проведенных рассуждений и построений. Зато несовпадение кривых вполне доказывает неверность полученного уравнения для кривой (, если, конечно несовпадение не связано с неточностью моделирования)..

Частичное решение задачи получения уравнения.

Иногда учащимся не удается получить уравнение для всех значений параметров, но удается получить уравнение кривой для какого-нибудь частного случая. Такие варианты также надо использовать и считать успешными.

Приведем пример такой работы, в которой уравнение получилось очень громоздким, зато один из очевидных частных случаев давал очень простое уравнение.

Рассмотрим фигуру, которую построил Сергей Грибовский (10-в, СУНЦ, 2005).

Алгоритм построения кривой:

Дана окружность с центром в точке О.
N - любая точка.
Точка В строится как пересечение окружности О и прямой NO
А - точка на окружности
М - точка пересечения прямой NA и окружности с центром N и радиусом АВ
Кривая - геометрическое место точек М при пробегании точкой А окружности, на которой она построена

Для некоторого частного случая (т.N совпадает с т.O) уравнение удалось существенно упростить, и тот же механизм дает более простую картину.

Заметим, что особенность кривой дает себя знать при геометрическом ее получении - строго говоря, нашим механизмом ее получить нельзя - ведь кривая пропадает при приближении точки С к точке В. Предельный случай придется переопределить отдельно, например, так: «если мышкой пододвинем точку N близко к точке O, у нас получится кривая, очень близкая к кривой более простой, а именно, когда вместо прямой NA берется просто горизонтальная прямая, а точка N сливается с точкой О».

Уравнение ее легко строится в полярных координатах, это

Если теперь на том же чертеже, где построена кривая, построить график кривой, то при подборе масштаба они совпадут при наложении. Кривая хорошо известна, но работа проводилась в самом начале обучения в СУНЦ, и учащиеся еще не изучали их.

Проверка наложением совпадения механической кривой и графика построенной по ней функции. Геометрический алгоритм Сергея Грибовского (10-в, СУНЦ,2005)

Пояснение. После вычислений формула, задающая радиус точки кривой в полярных координатах в зависимости от угла, была получена для частного случая кривой, и по ней построен график. Он оказался похож на график механической кривой. Для более точной проверки обе кривые были построены на одном графике. Теперь их можно наложить.

Кривая, построенная Александром Петровым.

Еще один пример - работа Александра Петрова(10в СУНЦ 2004/2005).

Его кривая задана несложно:

Дана окружность с радиусом АD и центром А.
На окружности построим точку В.
Проведем хорду ВD.
Перпендикулярно этой хорде из точки В проведем отрезок в направлении от центра окружности.
Длина отрезка берется равной радиусу. Пусть этот отрезок обозначен ВС.
Построим геометрическое место точек С при всех положениях точки В, то есть при ее движении по окружности.

Уравнение этой кривой находится из выражений для АС и угла DAC. Здесь естественным образом возникает смена параметризация кривой, так как сначала она определялась по углу DAB, а радиус-вектор ее уравнения направлен под другим углом - DAC. Но, как видно из рассмотрения получившихся треугольников, эти углы связаны простой закономерностью. А именно, угол DAC составляет три четверти угла DAB, и три угла BAC.

Если убрать требование задавать направление отрезку от центра, а откладывать радиус сразу в оба направления, то получится и вторая ветвь кривой, соответствующая полученному уравнению. Но математический опыт и интуиция учащихся 10-го класса еще не позволяют придумывать такие кривые сразу.

На рисунке оба варианта моделей - геометрическая и алгебраическая - сразу представлены на одном чертеже. Заметим, что совпадение кривых здесь неполное, так как геометрический смысл сдвоенных корней уравнения не раскрыт учащимся, но это пока и не требовалось - найденная функция действительно дает именно ту кривую, след которой вычерчивает придуманный учеником механизм, и еще некоторый «хвостик».

Кривая, алгоритм построения которой придуман Алексадром Петровым, (СУНЦ МГУ, 10в, 2005); ему удалось получить её уравнение и построить график.

Пояснение. При наложении кривые совпадают везде, кроме симметричной половины графика, которого нет на механической кривой. Если изменить алгоритм построения так, чтобы откладывать радиус сразу в оба направления, то получится и вторая ветвь кривой, симметричная первой, и соответствующая графику, построенному по уравнению.

(График на рисунке показан не полностью, он симметричен относительно оси абсцисс.)

Параллелограмм Уатта.

Кривые Уатта в математическом практикуме А.Н.Колмогорова.

Эта задача, по предложению В.В.Вавилова, взята из математического практикума ФМШ им.А.Н.Колмогорова. (А.Н.Колмогоров, В.В.Вавилов, И.Т.Тропин Физико-математическая школа при МГУ / Знание,М.,1981)

Само по себе историческое, это задание имеет еще и замечательную историю в СУНЦ МГУ (тогда еще 18-го интерната г. Москвы). Оно входило в «Математический практикум», созданный А.Н.Колмогоровым, конечно, в бескомпьютерном варианте - графики чертились на миллиметровке, а трудоемкость частично компенсировалась тем, что различные варианты (точнее, различные значения параметров) раздавались на целый класс, и потом только совмещались при анализе результатов. Ввиду принципиальной важности формы и содержания практикума для построения нашего курса, приведем текст [], где кратко описывется работа учащихся над этой темой.

«Параллелограмм Уатта - это шарнирный механизм, который был предложен Джеймсом Уаттом в 1774 году, когда он решал такую проблему - как связать поршень с маховым колесом, чтобы вращение колеса сообщало поршню прямолинейное движение?

Кинематическая схема параллелограмма Уатта, смонтированного на первой паровой машине (1769 г.).

Параллелограмм Уатта (вверху), как он смонтирован им на первой паровой машине (1769 г.).

Тщательно исследовав движение середины шатуна А1А2, Уатт (чисто эмпирически) убедился, что когда вся система в целом приходит в движение, эта точка незначительно уклоняется от прямой линии. Траектории движения этой точки (или точек, неразрывно с ней связанных) называются кривыми Уатта.

Перед учащимися ставилась задача исследования этих кривых. Сначала они вручную

(с помощью циркуля и линейки) выполняли следующее задание.

По заданным параметрам d, R, l плоского шарнирного механизма

а) начертите по точкам кривую Уатта, описываемую серединой шатуна (d=3, R=4, l=5)

б) на построенной траектории определите длину наибольшего участка кривой, отличающейся от отрезка менее чем на 5%.

При выполнении этого задания положение точки М отыскивалось учащимися так: поставив одну ножку циркуля с раствором 2d в некоторую точку Р окружности с центром в точке О1 радиуса R, найдем другой ножкой точку Q на второй окружности (с центром в точке О2 радиуса R); середина отрезка PQ определяется при помощи линейки.

Данное задание для многих учащихся явилось началом серьезного исследования: найти уравнение кривой Уатта, определить все возможные типы кривых Уатта, изучить, какие типы кривых получаются, если точка М каким-либо образом жестко связана с механизмом Уатта. Любую ли алгебраическую кривую можно начертить при помощи шарнирного механизма?

Заметим, что всего существует только 12 типов кривых Уатта (под типом мы понимаем ее форму). Задания учащимся раздаются таким образом, чтобы в итоге совместных усилий в каждом классе все типы кривых были вычерчены».

Межпредметные связи: кривые Уатта в математическом практикуме и спецкурсе по информатике.

Мы видим, что курс моделирования может взять на себя часть этой работы, а именно,

вооружить учащихся таким инструментом, что задача моделирования может быть продвинута значительно дальше, например, может быть снято ограничение рассматривать только симметрический случай R1=R2=R.

Виды кривых при различных вариантах жесткой связи также поддерживаются компьютерным моделирование, причем именно динамическое моделирование здесь наиболее удобно и наглядно - так как «поисковый» перебор вариантов жесткой связи удобнее всего делать с помощью мышки, размышляя над закономерностями, по которым видимо изменяется кривая Уатта..

Но и ручное построение имеет свои дидактические преимущества. Мы строим сначала простейший вариант тетради (а не на миллиметровке), а потом, почувствовав построение "пальцами", переходим к гораздо более точному построению по тому же алгоритму на компьютере.

Возможно, преподаватель математики предпочтет часть построения все же выполнить на миллиметровке, тогда нужно будет согласовывать программы курсов, так как ручное построение психологически выгоднее провести до компьютерного, а не после.

Многие задания математического практикума могут быть эффективно поддержаны курсом математического моделирования. Это требует взаимных согласованных усилий преподавателей информатики и преподавателей математики. Такая работа постоянно идет в СУНЦ МГУ, и в настоящее время математический практикум вновь начал свое существование, но уже в компьютеризованной форме.

Задача курса моделирования пересекается с задачей математического практикума в области технологии построения модели и методов ее визуального анализа. Но ставить математическую задачу детального анализа полученных кривых можно именно на математическом практикуме. Иначе говоря, это задача относится скорее к предмету математики, а не информатики. Здесь виден водораздел между двумя предметами Математическое исследование полученных моделей выходит за рамки сложности, допустимой для математических действий учащихся в курсе информатики, даже в профильном классе. На приведенных работах учащихся видно, что они действительно подбирали параметры модели скорее из эстетических соображений, с интересом знакомясь с множеством вариантов получающихся кривых и останавливаясь на наиболее запоминающихся формах.

Можно привести такое сравнение - к задаче о поездах из Москвы в Санкт-Петербург математика, физика и география подходят с совсем разных точек зрения, и это не значит, что какой-либо из предметов при этом страдает - наоборот, явление становится более объемным, более живым и осмысленным для учащихся.

Примеры работы с моделью параллелограмма Уатта.

Итак, компьютерное моделирование дает возможность возродить один из аспектов практикума, значительно снизив трудоемкость как вычерчивания следа механизма, так и построения графиков получающихся функций. Приведем для примера чертеж построения механизма Уатта и чертеж с несколькими вариантами параметров.

Построение модели механизма Уатта.

Пояснение. На чертеже показано, как строится механизм Уатта, при этом показан общий случай, когда значения длин (параметров) таково, что по ним можно построить два различных механизма, и изображены два положения шатуна 3.

Варианты кривой Уатта (длина выступа, задающего простейшую жесткую связь, равна нулю). Пояснение. Здесь собраны некоторые результаты работы с моделью параллелограмма Уатта по рассмотрению типов кривых Уатта.

Несколько работ учащихся 2005-2006 года, экспериментировавших со своими моделями параллелограмма Уатта.

Шарнирные механизмы П.Л.Чебышева и их моделирование.

Великий русский математик П.Л.Чебышев может считаться основоположником математического моделирования в России. И не только потому, что его математические конструкции входят в любой вузовский курс. Многие модели он воплощал буквально в бронзе, так как этот материал был самым удобным для вытачивания деталей шарнирных (и не только) механизмов. Эти факты могут дать увлекательный материал для проектной работы. Широко известны его «суставчатый механизм с задержками» и «стопоходящая машина». Из всех его механизмов, продолжающих тему "Параллелограмм Уатта" (над которой сам Чебышев долго работал), мы предлагаем включить в курс модель шарнирного механизма «с задержками».(Чебышев П. Л., Об одном механизме, Полн. собр. соч., т. 4, М,-Л., 1948.). Это пятизвенный механизм, превращающий вращательное движение не просто в движение по другой траектории, а в движение с задержкой. Это значит, что при движении точки В по окружности звено FE движется, а затем на некоторое время останавливается, затем снова движется и т.д. Происходит это оттого, что кривая, по которой движется точка М, имеет некоторый участок, очень близкий к дуге радиуса R=EM. Когда точка М движется по дуге радиуса R, звено FE неподвижно., когда она сходит с окружности на свою траекторию, звено начинает двигаться, и двигается, пока точка М опять не попадет на участок, близкий к окружности радиуса R (с центром, конечно, в точке E).

Чертеж «суставчатого механизма с задержками» П.Л.Чебышева

Пояснение. При движении точки В по окружности звено FE движется, а затем на некоторое время останавливается, затем снова движется и т.д.

Это происходит оттого, что кривая, по которой движется точка М, имеет участок, очень близкий к дуге радиуса R=EM. Когда точка М движется по дуге радиуса R, звено FE неподвижно.

Обоснование выбора модели механизма для курса.

Выбор этой модели обоснован двумя аргументами. Во-первых, эффектностью и неожиданностью движения механизма. Это педагогическое воздействие побуждает учащихся задуматься над секретами построения шарнирных механизмов. Во-вторых, опыт приближения дуги окружности частью кривой параллелограмма Уатта подводит к нескольким важным идеям - во-первых, к идее многопараметрической аппроксимации и идее равномерного приближения, а во вторых, к идее приближения формы кривой, независимо от масштаба. Ведь нужно получит именно горизонтальный участок кривой, а не приблизить ту или иную конкретную кривую или отрезок! Учащиеся почувствуют, что такая постановка задачи дает еще некоторые «степени свободы» при поиске решения, поскольку нужно найти не одно конкретное решение, а любое решение из множества. Точнее говоря, не просто подобрать кривую, на некотором интервале приближающую отрезок, а подобрать кривую, приближающую любой отрезок, лишь бы он был максимальной длины. Подбор же кривых осуществляется из уже знакомого им множества кривых Уатта, где жесткая связь с шатуном задается углом изгиба и размерами звена ВСМ. Именно эти идеи неявно определяют ход эмпирического поиска учащимися наилучшего соотношения длин звеньев и угла изгиба рычага. Наилучшее же соотношение параметров то, которое дает наиболее точную и длительную «задержку» одного из звеньев при непрерывном и равномерном вращательном движении «ведущего» звена.

Краткое поэтапное описание хода работы по теме.

После вводного рассказа и показа иллюстраций на доске рисуется схема механизма. Первый этап - построение модели и первая подгонка параметров - по кинематической схеме П.Л.Чебышева. Можно оставить включенным проектор, показывающий эту схему, или, наконец, раздать листочки с распечатанной схемой. Учащиеся строят чертеж механизма, а затем, глядя на схему, подправляют параметры так, чтобы достигалось подобие чертежа и схемы «на глаз».
Второй этап - экспериментальный подбор параметров. Длины звеньев корректируются таким образом, чтобы задержка механизма была наилучшей, то есть время неподвижности конечного звена должно стать максимальным.
Третий этап. После достижения некоторого результата модель достраивается - дополняется графиком зависимости угла поворота конечного звена от угла поворота начального звена. Теперь работа по уточнению параметров модели может быть продолжена, так как время неподвижности конечного звена соответствует длине горизонтального участка на графике, любое изменение длин и углов в модели автоматически отразится на графике, и подбор параметров облегчится.
Заключительный этап и домашнее задание (для желающих). Наконец, наилучшими наборами параметров учащиеся могут поделиться друг с другом, и, если есть время и возможности, полезно изготовить (например, на базе «Лего-конструктора») не виртуальную уже, а реальную действующую модель своего механизма.

Сочетание динамического графика и геометрической модели.

Перед Чебышевым встала задача: как подобрать простой шарнирный механизм так, чтобы участок траектории точки М был близок к дуге радиуса R? Чтобы сделать еще один шаг по направлению к математическому смыслу задачи, дополним модель динамическим графиком, то есть графиком, непосредственно реагирующим на все изменения в параметрах механизма.

Как и во многих других моделях, удачный подбор графика дает возможность добавить еще одно измерение, сделать моделируемое явление математически прозрачным. Особенно удачный вариант получается, если для движущейся по фиксированному закону (зависящему обычно от параметров) геометрической модели построить график зависимости положения моделируемой точки от времени.

Поскольку механизм переводит вращательное движение во вращательное, естественный график для него - график зависимости угла поворота конечного звена от угла поворота начального звена.

Модель построена для подбора подходящих параметров, максимизирующих задержку в механизме Чебышева (Насыров Ренат, 10-в, СУНЦ, 2005)

Бильярд в треугольнике и задача Фаньяно.

Обоснование выбора темы.

Бильярдные траектории - одна из геометрических тем, простых по постановке и первым результатам, но быстро выводящих на важные понятия современной математики. Эта тема также выбрана из соображений эффективности ее моделирования - погружение в нее удобно проводить именно на динамических моделях, сочетающих наглядность первоначальной постановки задачи с легкостью получения первых неочевидных результатов исследования. Кроме того, доказательства некоторых результатов также доступны для школьников.

Как задача моделирования в среде «Живая Геометрия» была предложена автору Г.Б.Шабатом на курсах МИУУ в 1996 году.

Постановка задачи.

В постановке задачи мы следуем А.Н.Землякову. (А.Земляков, Математика бильярда, «Квант»,1976, №5 стр.17-24).

Согласно законам механики, при отражении абсолютно упругого биллиардного шара от прямолинейного борта угол падения шара равен углу его отражения. Шар точечный, то есть, как говорят физики,"его размерами можно пренебречь".

Таким образом, мы считаем, что биллиардный шар - это движущаяся точка, и поэтому можно говорить о траектории биллиардного шара - о ломаной линии, по которой шар движется в соответствии с вышеприведенным законом упругого отражения. Точки излома этой ломаной лежат на «бортах биллиардного стола».

Наша модель будет построена для треугольных биллиардных столов. Более того, треугольник наш будет остроугольным.

Проблема биллиарда для нашей области заключается в том, чтобы найти ответы на такие вопросы:

Существуют ли периодические траектории?
Много ли их?
Как они устроены?
Как узнать, будет ли траектория, выходящая из данной точки в данном направлении, периодической или непериодической?
Как ложатся непериодические траектории в треугольнике?

И, конечно, по ходу изучения и расширения модели важно сформулировать и свои вопросы, которые необходимо научиться сразу фиксировать письменно.

Построение модели.

Ограничения модели.

Кроме остроугольности треугольника, мы наложим гораздо более жесткое ограничение на модель - будем рассматривать только те траектории, которые образованы последовательными отражениями от трех сторон в повторяющемся порядке:abcabcabcabc…

Для моделирования нам достаточно от 30 до 200 звеньев этой траектории - при меньшем количестве, чем 30, трудно будет сделать некоторые наблюдения, а большее, чем 200, только загромождает чертеж, не давая ничего принципиально нового.

Построение биллиардной траектории с помощью инструмента «отражение».

Самый простой способ построения модели - создание инструмента пользователя (личного инструмента, или сценария) и применение его вручную нужное число раз. Инструмент должен выполнять один шаг алгоритма. Здесь может быть два варианта - шагом можно считать одно отражение от очередной стенки, а можно шагом считать сразу три отражения подряд от трех стенок-сторон по порядку. Второй способ предпочтительнее, так как три одинаковых построения на различных сторонах сделать ненамного дольше, чем одно, зато применение такого инструмента будет намного более простым. Более того, от второго способа - прямой путь к использованию рекурсии в ее простейшем виде - в виде итерации.

Построение биллиардной траектории с помощью рекурсии.

Если мы построили алгоритм , отображающий две начальные точки, задающие направление первого «удара», на те же самые стороны, по закону движения биллиардного шара, то мы можем построить соответствующий итеративный процесс с помощью команды «Итерация» из меню «Преобразование».

Для этого выделим две точки, задающие направление движения, и выполним эту команду. В появившемся меню будет предложено отметить точки, в которые должны перейти при итерации исходные точки. Отметим точки, куда придет шар после одного полного "оборота" внутри треугольника, и в том же порядке. В том же порядке - значит, например, что начальной точке на стороне а назначаем в соответствие точку на стороне а, а точке на стороне b - точку на стороне b. При этом на чертеже проявится (выделенная более бледным цветом) траектория, получающаяся сразу после трех итераций. Иначе говоря, траектория при девяти последовательных отражениях от сторон треугольника.

Если учащиеся увидели, что траектория получается явно неверной (то есть не соответствующей закону упругого отражения), можно исправить модель, переназначив правильные точки для образов исходных точек. Если и это не помогает, надо отменить итерацию (кнопкой «Отменить»), и построить отражения еще раз так, чтобы требования команды «Итерация» были выполнены. Как правило, со второго-третьего раза у всех получается верная конструкция. Тем же, у кого все же никак не получается правильной траектории, можно помочь, предложив проконсультироваться у учащихся, верно построивших траекторию и хорошо понявших, как строится модель.

Особенности автоматизированного построения модели.

Когда и почему возникают особенности.

Если строить модель чисто геометрически и вручную, не возникает никаких сложностей, так как среда адекватно реализует построение циркулем и линейкой. Иначе говоря, если учащийся ясно понимает решение задачи на построение некоторой фигуры, то именно ее он и получит, без всяких неожиданностей.

Другое дело, если мы хотим сэкономить силы и время, и прибегнем к возможностям автоматизации построений. Все эти возможности вынужденно содержат ряд неявных соглашений, позволяющих отчуждать алгоритм от конкретного воплощения, и переносить его на другие объекты, то есть выполнять для других данных автоматически. Как правило, эти соглашения выбираются наиболее естественными, поэтому их даже не сразу можно обнаружить. Но тем не менее, возникают ситуации, когда их приходится учитывать - и обычно это требует некоторых искусственных дополнительных построений.

Именно такая типичная ситуация возникает с данным алгоритмом в среде Живая Геометрия. Рассмотрим ее подробнее.

Ситуация конфликта с решением, неявно принятым в среде моделирования.

Если мы попытаемся построить инструмент точно приведенным выше способом, и первым, и вторым, то обнаружим, что ничего не получается!

Инструмент не будет работать, а команду итерации не удастся заставить работать!

Анализ ситуации показывает, что происходит это оттого, что команда «создать новый инструмент» считает исходные точки, взятые на сторонах треугольника, случайными точками на соответствующих отрезках! И соответственно этому не вводит их в число аргументов созданного инструмента. Это неявное соглашение имеет ряд убедительных причин, анализ которых - отдельная и очень интересная задача. (И, конечно, тема для проекта или даже курсовой работы).

Но наша задача, вообще говоря, скромнее - построить правильно работающую модель!

Один из способов разрешения конфликта.

Сделать это можно, взяв в качестве исходного объект, заведомо попадающий в число аргументов инструмента или исходных точек итерации. Учащиеся СУНЦ предложили для этой цели создать отдельный движок, задающий положение начальных точек (начала и конца кия) на соответствующих сторонах треугольника. Это предложение учитывает одномерность параметра «положение точки на отрезке», но немного громоздко в реализации. Мы использовали другой прием, совмещающий решение сразу двух проблем - указанной проблемы и проблемы создания «ручки», или манипулятора для управления параметрами модели.

Искусственные элементы управления - «ручки» в геометрических моделях.

Дело в том, что движок, расположенный обычно в углу чертежа, из-за неявности своей связи с регулируемым параметром, психологически хуже воспринимается, чем «ручка», находящаяся в непосредственной связи с управляемой точкой.

Кроме того, в данной модели, как и во многих других, «ручка» необходима, чтобы в ситуации тесного расположения точек безошибочно потянуть именно ту точку, какую надо! При числе точек более трех (а их у нас, кстати, от 30-ти до 200) перебор соседних и мало различимых точек может быть весьма затруднителен!

В таких случаях обычную практику изменения чертежа с помощью перетаскивания «мышкой» его точек приходится дополнять. К такой точке, доступ к которой затруднен или невозможен, приходится присоединять искусственный элемент управления («ручку»). Его цель - производить необходимые перемещения, не теряя при этом наглядности и «непосредственности управления» геометрической динамической моделью. «Ручки» часто используются в «движках» (геометрический аналог реостатов), но иногда удобно их встраивать и непосредственно в чертеж.

Решение проблемы с помощью конструирования «псевдоручек».

Но все же создание «ручек» вместо исходных точек на сторонах треугольника может решить только часть проблемы. Дело в том, что созданная «ручка», конечно, станет частью исходных данных инструмента или итерации. Но тогда она же станет и объектом, который должен будет каждый раз воспроизводиться при автоматическом повторении процесса отражения! Ведь итерация включает в себя воспроизведение алгоритма построения «управляющего элемента», как и любого другого!

Методическое решение, предложенное нами для этого типа моделей, таково.

Ручка при применении инструмента или при назначении образа при построении итерации должна отобразиться (без потери общности) на управляемую точку.

Только тогда ряд последующих применений инструмента или повторений итерации даст нужный результат - единственную «ручку» при сохранении цепочки управления, то есть единственную ручку среди множества точек, каждая из которых является «редуцированной ручкой», невидимой в качестве ручки, но несущей необходимую информацию по положению точки на отрезке.

Конечно, не всякую «ручку» можно так отобразить. Назовем такую «ручку» «псевдоручкой», хотя это и не совсем точно - функции «ручки» у нее остаются.

Мы используем одну из самых простых реализаций этой идеи. Опишем её.

Конструкция простейшей «псевдоручки».

Возьмем свободную точку на плоскости, и опустим из нее перпендикуляр на нужную сторону треугольника. Нужна же нам та сторона, на которой расположится первая исходная точка траектории шара. Построим пересечение перпендикуляра и этой стороны, после чего спрячем перпендикуляр-прямую (по умолчанию строится именно прямая), и построим по двум этим точкам отрезок (это будет перпендикуляр-отрезок). То же проделаем и для второй исходной точки. При применении инструмента или отображении этим точкам можно сопоставить точки на сторонах треугольника(!). Это получается потому, что имеет смысл операция «опустить перпендикуляр из данной точки на отрезок» даже если данная точка уже находится на отрезке! То же относится и к операции «провести отрезок между двумя точками», - она имеет смысл, даже если обе эти точки уже находятся на отрезке и совпадают! Нам даже не очень важно, какой именно смысл имеет последняя операция - важно, что она не вызывает ошибки, и совместима в этом смысле с алгоритмом построения «ручки».

Об элементах объектного подхода и объектных средах проектирования.

Естественность и неизбежность применения таких рассуждений и таких, на первый взгляд, искусственных конструкций, исподволь подводит учащихся к понятию класса объектов. Происходит это оттого, что объектное мышление не противоречит законам конструирования в среде, и по простой причине - среда написана на С++ в соответствии с принципами объектно-ориентированного программирования. Тем из учащихся, кого заинтересуют детали строения классов, используемых в среде, можно порекомендовать ее упрощенный вариант - JAVA-плеер, прилагаемый к среде, но открытый для изучения и использования.

Итак, мы рассмотрели одно из неявных соглашений, принятых в данной среде проектирования.

И такие соглашения неизбежны в любой среде проектирования.

Более того, именно система этих соглашений и делает возможной «среду», как средство более высокого уровня по сравнению с набором базовых операций - в нашем случае построений циркулем и линейкой. Именно удачность, естественность этих соглашений во многом определяет удобство - а в конечном счете и успех такой «среды проектирования».

Исследования на модели треугольного бильярда.

Методика исследования модели, предлагаемая учащимся.

Данная модель характеризуется ясным механическим смыслом, и интуитивной прозрачностью. Эти свойства позволяют положиться на интуицию в исследовании модели. Так, мы даже не оглашаем вопросы, приведенные чуть выше в пункте "постановка задачи".

Как только получены работоспособные модели, мы предлагаем учащимся методику исследования. При этом говорится примерно следующее:

Изменяя все доступные параметры, отмечайте все достойные внимания варианты. Как только вы заметите на экране что-то интересное, немедленно сделайте «копию документа» через меню «файл» и команду «настройки документа». Затем оставьте лучшее и несовпадающее из собранного, удалив совпадающие или не лучшие варианты. Попробуйте расположить их в «естественной последовательности», перетаскивая мышкой имена страниц в окне «настройки документа». Назовите, пожалуйста, то, что остановило Ваше внимание, и попробуйте сформулировать связанные с этим предположения, если это получится (всё напечатать на чертеже). Попробуйте связать главное в получившихся конструкциях с известными Вам построениями и теоремами. Подпишите первую страницу (Имя , фамилия, класс, школа, год).

Конечно, такой подход возможен только в профильном классе, настроенном на проектную работу - в таком классе не задают после такой постановки задания вопросы "а что надо сделать?.."

Опорные математические результаты к уроку моделирования.

Задача преподавателя - поддерживать направлять и поддерживать поиск математически важных вариантов, и подсказывать те решения, которые не планируется получить самостоятельно.

Для данной задачи большинство учащихся получают чертежи правильного треугольного бильярда, сплошь заполненного траекториями, чертеж треугольной периодической траектории и чертежи периодических траекторий, состоящих из треугольников, подобных треугольной периодической траектории.

В этот момент можно поговорить о результатах, связанных с этими наблюдениями.

Во-первых, о том, что непериодическая траектория в правильном треугольнике (как, кстати, и в прямоугольнике) заполняет его всюду плотно (эти задачи называются еще задачами об освещаемости области (Гальперин Г.А. Земляков А.Н. , Математические биллиарды, М.: Наука, 1990).

Любая непериодическая траектория в правильном треугольнике всюду плотно заполняет весь треугольник.

Во-вторых, о том, что за треугольник получился как периодическая траектория. Опыт работы по его получению подсказывает учащимся, что для данного треугольника такая траектория единственная.

Здесь уместно дать некоторое время для наблюдений и проверки гипотез, что же это за треугольник. Обычно многие замечают (а некоторые даже знают) что это треугольник, построенный на основаниях высот исходного.

Гораздо менее очевидное утверждение о его экстремальных свойствах скорее всего придется пересказать учащимся. Хотя доказательство и здесь несложно, и можно наметить главный элемент доказательства - экстремальность траектории упругого отражения. Эта траектория, очевидно, кратчайшая из всех, соединяющих точку , откуда вылетел шар, и точку, куда он прилетел, при условии, что он должен "посетить" сторону, от которой отражается.

Важно связать этот математический результат с великим физическим законом - "принципом наименьшего действия" (в оптике он называется "принципом Ферма").

В нашей ситуации этот принцип можно сформулировать так - биллиардный шарик "умный", и из всех возможных траекторий выбирает самую короткую.

Этот принцип в случае треугольника приводит к знаменитой "задаче Фаньяни": если в данный остроугольный треугольник вписать треугольник наименьшего периметра, то вписанный треугольник дает периодическую биллиардную траекторию внутри исходного треугольника. Верно и обратное утверждение (при наших ограничениях).

Таким вписанным треугольником и оказывается треугольник, построенный на основаниях высот.

Несложный анализ распространит эти утверждения и на траектории, состоящие из того же треугольника, но "с уголками", причем эти "треугольные уголки" в какой-то момент совсем "поглощают" треугольник!

Проговор и фиксация наблюдений в письменной форме.

Важно научить учащихся проговаривать свои наблюдения, фиксировать их даже в такой, нестрогой и образной форме.

В этом, кстати, тоже резкое отличие курса моделирования от школьного курса математики, делающего принципиальный упор на абсолютной точности и строгости своих формулировок, и приучающем записывать утверждения именно в такой, точной и строгой форме.

Заметим, что эта задача, а именно проговор своих наблюдений, с каждым годом становится все более трудной для учащихся. Это наблюдение имеет ряд социально-психологических объяснений, но нам важно противостоять тенденции обеднения языка, так как здесь задача выговаривания неожиданной, ещё не сложившейся до конца гипотезы или наблюдения, напрямую связана с содержанием учебного курса моделирования.

Межпредметные связи на занятии.

Работа с этими математическими результатами служит задаче упорядочить и осознать полученный опыт моделирования, связать его с законами физики (или даже просто наметить эту связь). То есть все же главная задача для нас в курсе - задача информатики, задача практического освоения основ моделирования, в данном случае на материале механики и математики.

На занятие уместно принести раздаточный материал - например, оттиски статей из журнала "Квант", посвященные этой тематике. (Учащиеся СУНЦ обнаружат, кстати, что одним из авторов таких статей является… их собственный преподаватель геометрии, В.Н.Дубровский - и это тоже важный стимул, поддерживающий интерес к теме!). Впрочем, текст можно заменить ссылками на Интернет-адреса материалов, хотя раздача желающим бумажного варианта имеет свои (психолого-педагогические) преимущества.

Кроме того, у профильного класса (во всяком случае, в СУНЦ) есть возможности участвовать в спецсеминарах и спецкурсах для школьников, где также встречаются затронутые в курсе темы. Опыт моделирования помогает первичному ориентированию в темах, снимает первоначальный стресс погружения в незнакомые понятия, а иногда помогает и в исследовательских задачах.

Впрочем, здесь не надо преувеличивать практической роли курса - реальные задачи моделирования, выполняемые в профессиональных средах, мало похожи на наши учебные задания, как по методике работы, так и по решаемым проблемам. (см. ) Тем не менее базовые понятия моделирования всегда остаются теми же, и практический опыт любого компьютерного математического моделирования, полученный в школьные годы, остается источником вдохновения надолго.

Об ошибках и ошибках-открытиях.

В практической работе преподавателю очень важно научиться различать ошибки-опечатки и ошибки, происходящие от своеобразного, индивидуализированного видения задачи, не совпадающего с предлагаемым преподавателем. Обычно в школе нет возможности идти за каждым школьником (или даже за некоторыми) по его личному пути освоения новых понятий. В спецкурсе и элективном курсе такая возможность появляется, и это одно из важнейших их достоинств.()

Например, в работе по данной теме один из учеников СУНЦ (10-в, 2005) ошибся, и вместо модели отражения построил итеративную модель последовательного опускания высот на очередную сторону треугольника. С некоторой помощью преподавателя ему удалось продвинуть свое исследование, и получить простые, но вполне самостоятельные результаты, конечно, сильно отличающиеся от результатов одноклассников. Его итеративный процесс оказался сходящимся, причем довольно быстро. Рассмотрев периодическую траекторию (она оказалась единственной), он определил ее свойства, и вплотную подошел к доказательству сходимости. За остальное время урока он предпочел догнать своих одноклассников, но можно было и дальше продолжить изучать получившуюся у него модель.

Моделирование физических процессов

Эта тема содержит традиционные модели, методически хорошо проработанные в российской традиции преподавания информатики (см.2) :

Свободное падение брошенных тел с учетом сил сопротивления;
Задача двух тел;
Закон Кулона - поле двух зарядов, поле диполя, поле трех зарядов;

По сравнению с известными моделями, здесь мы достигаем двух важных результатов -

Ясности и скорости построения моделей
Легкости интерпретации из-за визуального их характера

Понятно, что первый результат обязан уже наработанному к этому моменту навыку геометрического моделирования, и без этого навыка он не будет достигнут.

Специфика этих моделей в том, что они могут быть построены двумя способами - как чисто геометрические модели, или как модели, включающие чисто алгебраические расчеты.

Те законы, которые определяют движение тел в этих моделях, естественно допускают чисто геометрическую интерпретацию. Вспомним, что закон тяготения выведен И.Ньютоном из законов Кеплера, сформулированных в геометрических терминах. Закон падения сформулирован Галилеем также в форме отношения длин пройденных путей.

Геометрически учащиеся легко построят отрезки, длины которых обратно пропорциональны друг другу, еще легче построить прямо пропорциональные. Здесь мы подробно разберем оба случая - и чисто геометрической модели (случай падения без учета сопротивления среды), и случай введения алгебраических расчетов в геометрическую модель.

Модель "Движение тела, брошенного под углом к горизонту"

Обоснование и построение модели.

Модель "свободное падение тела, брошенного под углом к горизонту," строится на занятии в два этапа.

Первый этап - построение модели 1, не учитывающей сопротивление среды.
Второй этап - построение модели 2, учитывающей сопротивление воздуха (в приближении линейной зависимости силы сопротивления от скорости).

И первая, и вторая модель построены в соответствии с рекомендациями не вводить дифференциальные уравнения, а строить разностную схему путем фиксации допущений о линейности процессов (Учебник, стр.416). Тогда первый шаг модели 1 строится таким образом :

1. Сначала напоминаем учащимся, что для малого промежутка времени Dt можно написать v=(Dx)/(Dt) , v=(x1 - x0) /Dt , причем чем промежуток времени Dt меньше, тем точность приближенного равенства выше.

В пределе при Dt -> 0 они становятся точным

В момент времени t1= t0+Dt будем иметь

x1=x0+v*Dt+ g*(Dt)2/2

При этом можно пояснить построение шага так:

Моделирование будет состоять в замене законов непрерывного физического процесса и описывающих его величин их дискретными аналогами.

Пока мы не будем подробно обосновывать правомерность этой процедуры, а приведем только наводящие рассуждения, поясняющие логику моделирования. Разобьем время процесса на одинаковые дискретные промежутки и заменим все непрерывные величины внутри промежутка на дискретные.

Пусть в первый промежуток времени Dt тело сдвинулось на вектор Dх в соответствии с начальной скоростью v0.

Если бы на тело не действовала сила тяжести, его скорость бы, в соответствии с третьим законом Ньютона, на изменялась, и в следующий момент времени Dt+Dt мы бы нашли тело в точке x0Dx+Dx. Геометрически это соответствует операции переноса точки В на заданный вектор, равный Dх.

Рассчитаем теперь положение тела в следующий момент времени, учитывая действие силы тяготения. По второму закону Ньютона, она изменяет его движение - тело падает с постоянным ускорением, которое называется ускорением свободного падения. Это значит, что за Dt его скорость изменяется на Dv, причем Dv/Dt=g

Это постоянное изменение скорости за время Dt изменит его координату на g*Dt*Dt/2 то есть на каждом шаге изменение вектора перемещения тела будет равно

Dx+g*Dt*Dt/2

Математическая модель построена. Ее реализация в среде виртуальной лаборатории очень проста:

Алгоритм геометрической реализации модели:

отложим вектор Dh=EF , направленный вертикально вниз
отложим вектор Dх=АВ и объявим его текущим вектором перемещения тела

(очередной шаг) -

от точки В отложим вектор ВС, равный Dх
от точки С отложим вектор СЕ, равный Dh
объявим текущим вектором перемещения тела Dх:=ВЕ и переименуем его в АВ
повторим очередной шаг 20 раз

Осталось пояснить, как связан вектор EF с вектором g*Dt*Dt/2.

Последний вектор на нашей «плоской» Земле практически не меняется и зависит только от шага по времени. Значит, EF, совпадающий с ним по направлению, равен c*g*Dt*Dt,где с - нормирующая константа.

Еще один важный параметр модели - масштабы единиц измерения по осям координат. Подбирая эти параметры, мы можем получать приближенные решения для заданных начальных условий. Но наша задача - не получить решение для конкретных значений начальной скорости и угла, а изучить качественный характер всего спектра решений, при всех возможных значениях параметров. Это значит, что нам важны не столько конкретные значения, сколько типичные значения! Что это значит? Это значит, что начальные данные, приводящие к сходным решениям, мы можем позволить себе не различать, объединяя такие решения между собой.

Степень сходства здесь можно выбирать, например, не различать решения, различающиеся только масштабом (одинаковые по форме кривой), или не различать решения, различающиеся только начальными данными, или различающиеся сдвигом по оси координат и т.п.

Один из эффективных приемов, позволяющих решать такую задачу, называется "обезразмериванием". Он состоит в специальной форме параметризации модели, когда в качестве ее параметров берется безразмерное отношение некоторых параметров, или другая их безразмерная функция.

По (Учебник, стр. 420) обезразмеривание заключается в том, чтобы "вместо абсолютных единиц системы СИ перейти к относительным единицам, естественным именно для данного движения ... Важнейшая роль обезразмеривания - установление законов качественного подобия".

Таким образом, построенная нами модель также может рассматриваться как безразмерная, если для нас неважно, какими в данный момент единицами измерения мы пользуемся, а важна только качественная картина явления.

Тогда можно считать, что сдвигая Dh и изменяя длину начального отрезка Dх, мы меняем величину шага по времени и модуль начальной скорости, а угол наклона вектора Dx относительно горизонта отражает этот же параметр модели.

Таким образом, мы получили алгоритм построения точки по заданной точке и двум векторам, при этом один из векторов является для траектории неизменным.

Геометрически это сводится к указанию мышкой двух предшествующих точек траектории и получении в результате следующей.

Представление алгоритма на внутреннем языке.

Среда “Живая Геометрия” имеет внутренний язык, на котором можно получить запись построенного алгоритма шага моделирования. Он также локализован нами (3-я версия ЖГ, 4-ая - с участием А.В.Чехловой), и получающийся текст доступен для понимания без всякого обучения. Вот как выглядит на нем эта запись.

Окно сценария инструмента построения шага модели.

Пояснение. Сценарий - автоматизированное отделение алгоритма построения фигуры от ее чертежа. Шаги алгоритма исчерпывающе описаны. Данными (исходными) являются точки A,B,C,D. Из них заново (вручную) нужно задавать только А и В, поскольку C и D помещены в раздел «вызываемые по имени на чертеже», и вызываются автоматически. Этот алгоритм содержит 5 внутренних шагов, из них 3 шага - построения отрезков между двумя точками.

Нужное число шагов невелико, довольно лишь 15-30, чтобы проследить все особенности поведения модели. Поэтому мы строим каждый шаг вручную. При использовании построенного инструмента (содержащего алгоритм одного шага) для получения очередного звена ломаной нужно щелкнуть мышкой два раза - отметить две точки из пункта Данные окна сценария построенного инструмента.

Модель свободного падения тела.

Пояснение. Для построенная с помощью инструмента потребовалось 11 раз рекурсивно его применить, вручную отмечая каждый очередной отрезок. Если требуется большое количество применений, используется аппарат терминальной рекурсии из меню «Преобразования» (см. Выше параграф «Рекурсия»).

Большинство виртуальных геометрических лабораторий позволяет повторять некоторый алгоритм построения автоматически или полуавтоматически (когда часть данных на каждом повторении строится явно или указывается мышкой). ЖГ также позволяет это делать. Можно автоматизировать этот процесс через команду Итерации, которая позволяет делать глубину итерации (терминальной рекурсии) параметром.

Чтобы не перегружать технической информацией первые занятия, мы остановились на полуавтоматическом варианте, когда повторно применяется созданный инструмент построения одного шага. Все же половина данных вызываются автоматически, по наименованию на чертеже (см. Рис.7 “Объекты на чертеже”), и только две точки нужно отмечать на каждом шаге вручную (см. Рис.7 “Данные”). Заметим, что звеньев траектории нужно обычно не более 20-ти.

Падение в среде с сопротивлением воздуха.

Переход к модели 2 очень прост - вводится сила сопротивления воздуха, при этом схема рассуждений остается точно такой же. К результату шага модели 1

добавляется еще один вектор смещения в направлении -v /|v| , по величине пропорциональный |v| . Коэффициент пропорциональности равен c*k, с - нормировочная константа, k - коэффициент сопротивления воздуха, в приближении f=-kv (это приближение, как известно из физики, работает при относительно малых скоростях, при ламинарности возникающих потоков). Коэффициент пропорциональности мы задаем в виде отношения двух отрезков,

Рис.8 Задание коэффициента сопротивления воздуха отношением отрезков.

и в заданном так отношении делим результат шага по первой модели:

Построение шага с учетом сопротивления воздуха.

В результате алгоритм построения одного шага (одной итерации) будет таким:

Окно сценария инструмента #2 построения шага модели с учетом сопротивления среды.

Пояснение. Шаги алгоритма исчерпывающе описаны. Данными (исходными) являются точки A,B,C,D,E,F,G,H. Этот алгоритм содержит 8 внутренних шагов. Здесь три четверти данных вызываются автоматически, по наименованию на чертеже ( “Объекты на чертеже”), и только две точки нужно отмечать на каждом шаге вручную (“Данные”).

Повторяя этот шаг 15 раз, получаем кусочно-линейное приближение траектории тела.

Модель падения тела с учетом сопротивления среды.

Пояснение. Для построенная с помощью инструмента потребовалось 15 раз рекурсивно его применить, вручную отмечая каждый очередной отрезок.

Заметим, что один из школьников (Алексей Калиниченко, 10-в, 2000 г.) при выполнении домашнего задания обратил внимание, что его модель при изменении угла наклона “пушки” делает движение, похожее на движение крыла. Он положил эту траекторию в основу крыла и хвоста, второе крыло и вторая половина хвоста получились в результате отражения относительно “оси птицы”. Несколько штрихов, дополненных механизмом возмущения траектории - и при движении начальной точки по окружности “птица” изящно машет крыльями! Параметры «птицы» и её движений подбираются мышкой.

Таким образом родился и был самостоятельно выполнен небольшой проект. Из сравнительно точной модели падения тела ученик сделал очень очень приблизительную, но красивую “биологическую” модель - модель полета птицы.

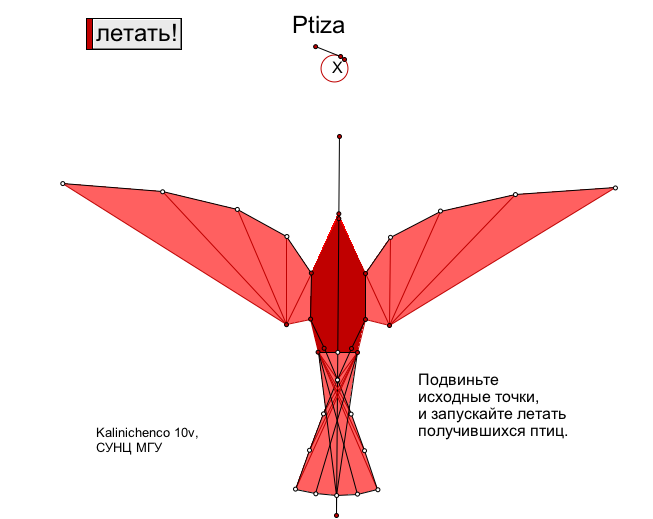
Птица - побочный продукт модели движения тела. Модель создана Алексей Калиниченко, 10-в, СУНЦ 2000 г.

Кстати, в список опубликованных работ школьников СУНЦ вошла и другая “эстетическая модель ” совсем другого генезиса - модель “ЗАЧЕТ”, (Артем Попов,2000 г.) уже не имеющая исходного физического смысла, и рожденная по чисто эстетическим критериям как несложная модель синтеза движения по трем дугам.

Модель эстетической направленности - разноцветные следы отрезков прямых, связанных со скользящими и разгибающимися дугами. Создана Артемом Поповым, 10-в СУНЦ, 2000г.

Исследование построенных моделей.

Грубая прикидка правильности построения.

Правильность первой модели проверить легко - аналитическое решение этой задачи детально изучается в школе, и ошибки построения модели сразу заметны.

Самый простой путь проверки - на том же чертеже вызвать команды построения графика, задав у= - х2. Двигая мышкой оси координат и единичный отрезок, можно наложить график на траекторию и убедиться в их эмпирическом совпадении на видимом интервале. Конечно, в случае правильного построения модели.

Нужно подчеркнуть, что такая проверка не доказывает совпадения, хотя может доказать несовпадение (если таковое наблюдается), т.е. неверность модели.

Правильность построения второй модели может опираться на правильность первой, так как предельный случай второй модели дает первую модель, при нулевом значении коэффициента сопротивления среды. При большом значении коэффициента сопротивления траектория короткая. И наконец, физические соображения дают и примерную форму кривой - поначалу близкая к параболе, она круче в области “падения” тела, т.е. асимметрична.

Качественный анализ явления по модели.

Модель 2 дает несколько содержательных выводов, допускающих ясную физическую интерпретацию. Они могут быть оформлены как мини-проекты.

стрельба из пушки (баллистическая траектория) - здесь можно проследить зависимость предельной дальности стрельбы от угла наклона и зависимость точности стрельбы от ее дальности (можно оформить ее как игру).
прыжок с парашютом - для этого угол “броска” выбирается нулевым, а начальная точка поднимается на некоторую высоту. Парашют здесь “раскрывается” сразу, но можно создать модель, когда сопротивление среды в некоторый момент резко возрастает. Тогда можно подбирать момент раскрытия парашюта для заданной скорости приземления (тоже можно оформить как игру)

В (2) предлагаются и другие вариации этой темы, которые можно использовать для проектной работы.

Дополнительные построения для анализа модели.

Полезно построить динамические графики полета тела для некоторого множества начальных значений. Проще всего его задать отрезком, по которому скользит точка, определяющая это значение.

Приведем примеры таких графиков.

Модель представляет форму траектории при различных значениях коэффициента сопротивления в случае F= -kv .

Получаем динамический спектр траекторий при вариации начальной скорости.

Получаем динамический спектр траекторий при вариации угла наклона.

Строя совместные динамические графики, удобно изучать качественную картину поведения модели.

Модель “Закон Кулона”

Эта модель строится немного иначе, хотя в основе - тот же пошаговый алгоритм метода Эйлера.

Тот же способ обезразмеривания и гибкости подбора коэффициента масштабирования, что и в модели падения, применяется и в этой модели.

Коэффициент в законе Кулона, соответствующий коэффициенту в формуле второго закона Ньютона для падения, также задается отрезками, а точнее, отношением их длин. Масштаб задается из соображений удобства наблюдения явления на чертеже. “Обезразмеривание” происходит так же и с теми же целями, что и в модели падения.

По закону Кулона, сила взаимодействия обратно пропорционально квадрату расстояния и прямо пропорциональна величинам зарядов. Значит, наш коэффициент пропорциональности содержит и масштабные множители, и величину пробного заряда, и коэффициент в законе Кулона, Все это мы можем полагать изменяющимся, перемещая движок, длина которого и есть изменяющийся множитель, регулирующий все эти величины.

Спрятав ненужные уже построения, мы оставляем исходные объекты, и конечные объекты. Теперь можно дать команду программе запомнить алгоритм получения конечных объектов из начальных. Это команда “Создать новый инструмент” в специальном меню инструмента :

Теперь нужно разделить аргументы полученного алгоритма - одни вызываются по имени, которое ищется на данном чертеже, другие формируются мышкой - либо строятся, либо указываются.

Это делается щелчком мыши в разделе “Объекты на чертеже” в окне сценария.

Щелчок на имени объекта вызывает появление окна его свойств, и для аргументов, не изменяемых в процессе применения инструмента, нужно выставить флажок для свойства “Соответствует объекту с тем же именем на чертеже”.

Теперь в разделе “данные” сценария инструмента “шаг Кулона” остался только один аргумент - точка, в которую помещается пробный заряд. Поэтому от курсора отходит отрезок, пропорциональный вектору силы кулоновского взаимодействия.

Если поставить курсор в конечную точку уже имеющегося отрезка, и нажать кнопку мыши, работа инструмента будет завершена, и мы будем иметь уже два звена ломаной, приближающей силовую линию электростатического поля. Построим 10-20 звеньев. Теперь мы можем из любой точки посмотреть, куда и как идет силовая линия.

Это тот же метод Эйлера. И здесь доказательство его применимости (сходимости к решению) мы оставляем, хотя уместно указать на необходимость такого доказательства.

А если установить режим “оставлять след”, мы можем получит на чертеже всю картину силовых линий поля двух зарядов, вручную или автоматически.

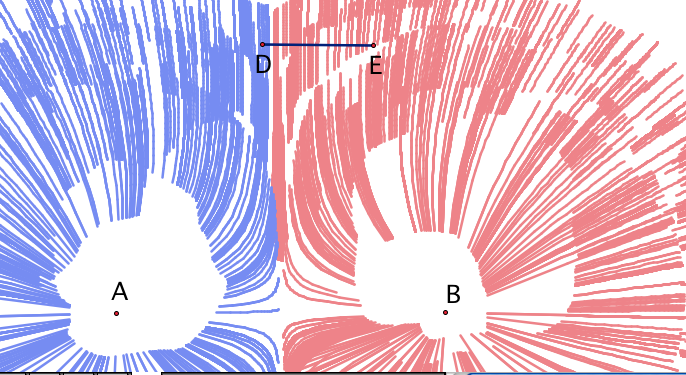
Работа с моделью силовых линий электростатического поля двух одноименных зарядов - ломаная, приближающая силовую линию, оставляет след при движении "точки исходного положения пробного заряда". Двигаем точку вручную.

Если изменить масштаб. мы получим “поле двух зарядов”. Один из простых “численных экспериментов” - сравнить поле одного и поле двух зарядов наложением. Мы видим, что, начиная с некоторого радиуса, они почти неразличимы.

Дальнейшая работа с моделью состоит в усложнении моделируемых конфигураций - модели диполя, квадруполя, и т.п. могут легко быть получены учащимися, построившими инструмент для простейшей модели.

На чертеже Воронина (10-в СУНЦ 2005) хорошо видны траектории, вычисленные с ошибками - в данной модели такое бывает, когда нарушаются требования соотношения шага и точности. С этими соотношениями мы знакомимся "эмпирически", без вывода соответствующих формул.

Настройка модели с помощью изменения величины "шага по времени".

При прохождении "модельной" силовой линии вблизи от особых точек (точек, в окрестности которых нарушается непрерывность моделируемых величин) будут заметны характерные "изломы", явно не соответствующие поведению силовой линии. Это происходит оттого, что вблизи таких точек нарушается предположение об относительной малости шага по сравнению с масштабом изучаемого явления, и, следовательно, возможности его линейного приближения. Мы не строим в курсе модели с переменным шагом (такая тема может быть темой проекта), но понимать, что переменный шаг в таких случаях необходим, учащимся поможет следующее наблюдение.

Модель электростатического поля А.Петрова (СУНЦ 2005, 10-в). Видны и регулярная часть модели, и "выбросы" - ошибки моделирования рядом с особыми точками.

Если такой ситуации уменьшить шаг, то при некотором его значении "изломы" пропадут. Платой за это будет резкое уменьшение длины моделируемого участка силовой линии.

Переменный шаг дает возможность "компромиссного" решения - и оставить длину моделируемого участка на "гладких" местах достаточно большой, и не допустить срыва моделирования вблизи "особых точек".

Конечно, эти замечания относятся ко всем моделям с "особыми точками", а не только для моделей "из физики".

Задача двух тел.

Задача двух тел - классическая задача на применение закона гравитации. Она, как известно, еще имеет (в случае 2-х тел) аналитическое решение. Мы построим приближенное решение тем же методом Эйлера, сначала в случае двух тел равной массы, а затем, уже в процессе самостоятельной работы учащихся, трех и более тел различной массы.

Ход работы очень близок к описанному в двух предыдущих моделях.

Построение инструмента, выполняющего очередной шаг метода.

По двум начальным положениям тел и векторам скорости строим следующий шаг - следующие два вектора, дающие две новые конечные точки. Параметром является отрезок, задающий масштаб.

Построение модели.

С помощью инструмента вручную построим 30-50 шагов алгоритма.

Проведение экспериментов.

Теперь проводим эксперименты с моделью, изменяя начальные значения и масштабный параметр, фиксируя различные полученные конфигурации траекторий и интерпретируя их.

На этом этапе целесообразно привлечь учителя физики для формулирования содержательных заданий для моделирования в рамках построенной модели, проведения модельных исследований и интерпретации получаемых результатов. Из удачных работ этого типа возникают проектные работы под двойным руководством - преподавателя физики и преподавателя информатики.

В зависимости от векторов начальной скорости траектории будут принимать знакомый физикам и астрономам вид.

Глава 3

Педагогический эксперимент и другие формы верификации результатов исследования.

Об апробации практикума.

Основные положения и результаты исследования обсуждались на:

научной конференции МГПУ <Проблемы активизации

учащихся> (г.Москва, 2002 г);

научной конференции МГПУ <Конференция молодых ученых

> (г.Москва, 2000 г);

научной конференции факультета математики

Московского педагогического государственного университета (г.

(г. Москва, 2002 )

научно-методическом семинаре МЭИ < Использование компьютерных

средств в преподавании математики> ( 2001 г.);

заседаниях кафедры ИПМ Московского Городского педагогического

университета (г. Москва, 2000 гг.);

заседаниях кафедры информатики СУНЦ Московского Гсударственного

Университета (г. Москва,

2002 гг.);

научно-методическом семинаре ФПО Московского Гсударственного

Университета (г. Москва, 2002, 2004 гг.);

заседаниях кафедры математической физики Московского Государственного педагогического университета (г. Москва, 1998-2006)

гг.);

конференциях ИТО

По теме диссертации опубликовано 6 работ.

Апробирован спецкурс «Практикум по математическому моделированию» в СУНЦ МГУ (10-11 кл) (2000-2006 г.г.)

апробирован спецкурс для педвузов "Учебное моделирование в

виртуальном конструкторе Geometer's SketchPad" в МГПУ (2000-2002 г.г.)

Разработана и внедрена программа 12-часовых, 24-часовых и 72-часового блока «Компьютерные средства в преподавании математики («Живая Геометрия») для курсов повышения квалификации учителей, апробирована и внедрена в МИПКРО (1999-2001 г.г.), МИОО (2002-2006 г.г.).

Апробация практикума была проведена на двух основных площадках и двух дополнительных.

Основные площадки:

Профильная школа (спецшкола)
Курсы повышения квалификации учителей

В качестве профильной школы был выбран СУНЦ МГУ, в качестве курсов - курсы МИПКРО (МИОО).

Дополнительные площадки:

Педагогический ВУЗ
Средняя школа

Апробации проходила в МГПУ (математикческий факультет, 2001-2002 г.г.) и МПГУ (физический факультет, 2002-2003 г.г.) и в 542 (общеобразовательной) школе г.Москвы.

Кроме того, основная часть методических материалов практикума прошла апробацию в рамках апробации УМК «1С Математика 5-11, практикум», организованного НФПК в 2003-2004 г.г.

Заключение

Диссертационное исследование было вызвано практической необходимостью - построением элективного спецкурса «математическое моделирование» для кафедры информатики СУНЦ МГУ. В ходе исследования были получены результаты, относящиеся к методике преподавания информатики, в том числе построен оригинальный тип заданий - «черные ящики».

Эти результаты были применены в работе над проектом УМК «1С Математика 5-11, Практикум» для конкурса НФПК по заказу Минобразования (научный руководитель - В.Н.Дубровский). Проект выиграл конкурс и был реализован в 2001-2005 году, пройдя все запланированные стадии разработки и внедрения, в том числе и апробацию.

Целью работы было повышение эффективности практикума по матмоделированию. Решалась задача выбора МО, подбора системы заданий и построения её методического обеспечения, обеспечивающих планируемое повышение эффективности.

Основная гипотеза исследования состояла в том, что выбор виртуального геометрического конструктора в качестве базового МО для спецкурса и опора на алгоритмы конструирования, знакомые учащимся по школьному курсу планиметрии, и визуально-манипулятивные способы построения и исследования позволят создать эффективную систему заданий по моделированию с элементами проектной работы.

Таким образом, после подготовительной работы, состоявшей в знакомстве с различными типами практикумов по математическому моделированию, применяемым МО, монографиями, учебниками, статьями и документами Министерства образования по этой теме, была поставлена и решена двуединая задача, связанная с формировнием набора заданий и методики работы с ними. С одной стороны, математически содержательные задачи, выбранные для моделирования, требовалось так перестроить, чтобы наиболее естественным способом работы с ними было конструирование и исследование в среде учебного виртуального геометрического конструктора. С другой стороны, требовалось так подобрать задачи, их постановки и предлагаемые пути решения, чтобы они покрывали запланированную часть материала по математическому моделированию на уровне формирования навыков применения этих понятий.

Таким образом, выполнение этого плана привело к замене преимущественного типа практической работы - вместо работы с текстами выполняется работа с наглядной моделью плоскости (компьютерными аналогами механических инструментов - циркуля, линейки, карандаша и т.д.) Так же и исследования полученной модели переводятся из текстовой формы в манипулятивную и визуальную форму, а главным исследовательским механизмом является визуальное обнаружение инвариантов полученной модели при различных заданных конструкцией допустимых движениях, подбираемых в поисковой деятельности.

Такая замена приавела в ряде случаев к формированию новых типов заданий, не встречавшихся в статическом или текстовом варианте. Наиболее важным типом таких заданий является тип заданий «геометрические черные ящики». Он реализован и на диске «1С математика 5-11. Практикум.» Вот как его описывает В.Н.Дубровский:

“...Особый класс экспериментальных заданий составляют задачи с «черном ящиком». На экране показаны какие-то объекты; одними из них можно управлять, положение других при этом изменяется по неизвестному (!) правилу. На «эмпирическом» уровне требуется (подбором) добиться заданного расположения объектов. На более высоком, «теоретическом» уровне нужно разгадать зависимость между объектами. Один из циклов таких заданий состоит из своего рода математических головоломок разных видов. В другом, преследующем более конкретную учебную цель, предлагаются пары фигур, одна из которых является образом другой при каком-то геометрическом преобразовании; его-то и надо восстановить. В таких заданиях с наибольшей четкостью реализованы в своей взаимосвязи важнейшие компоненты научного исследования - анализ и синтез. Впрочем, почти любая представленная в практикуме модель дает повод к такому исследованию: понять, как она построена, и построить ее самому - эта задача почти всегда будет интересна и поучительна с математической точки зрения.” (8,9)

Второй тип заданий, полученный в ходе исследования - «задачи с динамически обусловленной подсказкой». Его идея восходит к давним дидактическим работам А.А.Кузнецова о гибком применении подсказок в компьютерных обучающих программах. Но она реализована в особой среде виртуального конструктора геометрическими методами, что потребовало некоторого методического её уточнения, и учета гораздо большей гибкости геометрических моделей, чем у тех обучающих программ, о которых шла речь в конце 80-х годов.

Также выделены некоторые полезные методические принципы построения работы учителя и учащихся в используемой компьютерной среде и близких к ней по идеологии.

Последний из методических результатов, который хотелось бы упомянуть, это методика фиксации и связанному с ней переходу к текстовому способу записи результатов исследования модели. На этом этапе найден эффективный метод использования механизма автоматического протоколирования работы, встроенного в большинство современных виртуальных конструкторов, начиная с «МИКРОМИРа-85». Этот механизм обычно позволяет возвращаться к любому из предыдущих этапов работы, сохранять его, и продолжать работу с любого этапа. Поскольку высокая поисковая активность - основной дидактический прием практикума на базе манипулятивных и визуальных средств, то учащиеся за короткое время успевают перебрать десятки и сотни вариантов. Конечно, последовательная ручная фиксация в таком случае немыслима. Можно научить учащихся отбору среди пройденных этапов наиболее существенных и показательных, нуждающихся в фиксации и минимальных комментариях промежуточных результатов. Слово «промежуточный результат» в исследовательской работе может не иметь смысла, если не имется в виду достижение однозначного «конечного результата», или до него ещё далеко. В таких случаях целый ряд результатов нужно считать «окончательными», так как часто сразу неясно, как они упорядочены по их «окончательности». Все их желательно ввести в презентацию работы по моделированию. В простейшем случае она является кратким описанием модели с набором «страниц» с полученными вариантами моделирования. Всё это снабжено минимальным аппаратом презентирования - надписями, кнопками показа дополнительной или скрытой информации, кнопками анимации и кнопками ссылок (на соседние страницы или в Интернет).

Построенные учащимися динамические визуальные модели могут быть конвертированы в JAVA-апплеты и отредактированы как интернет-страницы, но эта работа выходит за рамки нашего краткого элективного курса (24 или 32 часа), и может быть проведена только как проектная.

Образцы подобных страниц можно увидеть среди работ бывшей студентки-участницы аналогичного спецкурса нашей кафедры в МГПУ, теперь уже преподавателя, Ксении Алексеевны Николаевой.

Апробация методических решений, примененных в элективном курсе, проводилась НФПК в рамках апробации продукта, заказанного «1С» и ИНТ, а также в СУНЦ МГУ, в течении шести лет функционирования спецкурса-практикума, который вел автор. Результаты внедрены в СУНЦ МГУ и в МИОО.

Литература:

А.А. Кузнецов, Л.О. Филатова Информатика в профильной школе // Информатика и образование.- 2003.- N 6.- C. 14-18.
Роберт И. В. Современные информационные технологии в образовании: дидактические проблемы; перспективы использования. // М., 1994.
Белошапка В.К. Информационное моделирование в примерах и задачах.//- Омск: Из-во ОГПИ, 1992.
Цукарь, А.Я. Дидактические материалы по геометрии с элементами исследования для 7 класса // М.: Просвещение, 1998. - 79 с.
С. Бешенков, Е. Ракитина, Моделирование и формализация. Методическое пособие // М.:ЛБЗ,2002,-336 стр.
Шабат Г.Б. О компьютерном эксперименте в преподавании математики // "Монитор-Аспект", 1995, 6. - с.122-125.
В.Н. Дубровский, А.В.Земляков, А.В.Пантуев, А.В.Чехлова и др., Образовательный комплекс"Математика, 5-11 классы. Практикум", ЗАО"1С", 2003.
В.Н. Дубровский “Практикум - новая форма электронного образовательного издания по математике”// сб.докладов Международной конференции ИТО-2003. М: РУДН, 2003, с.65-69.
В.Н. Дубровский “СТЕРЕОМЕТРИЯ С КОМПЬЮТЕРОМ // Компьютерные инструменты в образовании. - СПб.: Изд-во ЦПО "Информатизация образования", 2003, №6, С. 15-23.
А.В. Пантуев “Виртуальные лаборатории и активизация работы школьников” // сб. “Стимулирование познавательной деятельности студентов и школьников”, М: МГПУ, 2002, с. 30-33.
Фалина И.Н., Андреева Е.В, Математические основы информатики. Элективный курс. //Элективные курсы в профильном обучении: образовательная область “Математика”/Министерство образования РФ - Национальный фонд подготовки кадров. -М.,Вита-Пресс, 2004 (http://www.profile-edu.ru/files/1_04_04/Matematika.pdf)
Выготский Л.С. Орудие и знак в развитии ребенка // Собр. соч. Т. 6. М.: Педагогика, 1984.
Поздняков С.Н. Геометрия в движении (с компьютерной поддержкой). СПб.: ЦПО "Информатизация образования", 1995.
Храповицкий И.С. Эвристический полигон для геометрии // Компьютерные инструменты в образовании, 2003, 1.
Иванов С.Г., Поздняков С.Н. Компьютер в продуктивном обучении математике. "Комьютерные инструменты в образовании" 5, 2003 г.
Вопросы психологии учебной деятельности младших подростков. / Под ред. Д. Б. Эльконина, В. В. Давыдова. - М.: Изд-во АПН РСФСР, 1962. - 287 с.
Гальперин П. Я. Психология мышления и учение о поэтапном формировании умственных действий // Исследования мышления в советской психологии / Отв. ред. Е. В. Шорхова. - М., 1966. - С. 236-277.
Пантуев А.В. "Классификация средств интегрированной среды "Живая Геометрия" по типу занятия", сб."Дни науки МГПУ-2001 г." , МГПУ,2001 г.183 с., стр.105-107.
Давыдов В.В. Теория развивающего обучения. - М., 1996.
Беспалько В.П. Слагаемые педагогической технологии. - М., 1989.
Пойя Д. Математическое открытие. - М.: Наука - 1976.
Амонашвили Ш.А. Личностно-гуманная основа педагогического процесса. - Минск, 1990.
Шаталов В.Ф. Куда и как исчезли тройки. - М.: Просвещение, 1990.
Соловейчик С.Л. Педагогика для всех. М., 2000.
Эльконин Д.Б. Психология игры, М., 1978 г.
Шаталов В.Ф. Опорные конспекты по кинематике и динамике. - М.: Просвещение, 1989.
Библер В.С. Мышление как творчество. - М., 1975.
Гусев В. Геометрия. - М.: Авангард, 1996.
Давыдов В.В. Теория развивающего обучения. - М., 1986.
Потоцкий М.В. О педагогических основах обучения математики, М., 1963ъ
В.А.Успенский Семь размышлений на темы философии математики, в сб. «Закономерности развития современной математики», М.,Наука, 1988
В.П. Зинченко Психологические основы педагогики М.: Гардарики, 2002).
Талызина Н. Ф Педагогическая психология:.М.,«Академия»,2001
Лапчик М.П.,Семакин И.Г., Хеннер Е.К. Методика преподавания информатики, М., «Akademia», 2003. - 624 с.
Юдина А.Г. Практикум по информатике в среде «LogoWriter»: учебное пособие для общеобразовательной школы. - М.,ИНТ, 1997.
"Роботландия 96", пособие для учителя - Роботландия, Переславль-Залесский, 1996

Ландо С.К., Семенов А.Л. Учебная программа «Алгоритмика»:5-7 классы, - М., ИНТ, 1997.

Кушниренко А.Г., Лебедев Г.В. 12 лекций о том, для чего нужен школьный курс информатики и как его преподавать. : Методическое пособие .- М.: Лаборатория базовых знаний, 2000 (Вологда: Полиграфист, ПФ).- 464

Семакин И.Г., Шеина Т.Ю. Преподавание базового курса информатики в средней школе : Методическое пособие . - Лаборатория базовых знаний , 2002

Челак Е.Н., Конопатова Н.К. Развивающая информатика : Методическое пособие . - Лаборатория базовых знаний , 2001

Table of Contents