ЧЕРНОВИК

ДИССЕРТАЦИИ

13.00.02 - теория и методика обучения и воспитания
(информатизация образования, информатика)

диссертация на соискание ученой степени
кандидата педагогических наук

Пантуева Андрея Валерьевича

Методические проблемы построения элективного курса-практикума по математическому моделированию для профильных классов в среде Geometer's SketchPad.

Москва - 2004

Работа выполнена на кафедре информатики Московского Городского Педагогического университета.

Научный руководитель:

доктор педагогических наук, профессор А.С.Лесневский

Официальные оппоненты:

доктор физико-математических наук, профессор Н.Х.Розов (МГУ)
кандидат педагогических наук, доцент С.В.Бирюков (МПГУ)

Глава 2

Методические комментарии к избранным темам практикума по математическому моделирования.

Планиметрия

Критерии отбора планиметрических тем.

Выбор планиметрических тем подчинен тем же принципам построения эффективного курса моделирования (а не курса планиметрии). Уточним эти принципы на материале планиметрии.

Учебная эффективность для курса информатики.
Ясная и доступная формулировка задачи.
Прозрачность логики построения математической модели задачи.
Доступность (для всех учащихся) самостоятельного исследования поведения модели.
Возможность интерпретации поведения модели
Возможность построения гипотез о решении задачи.
Нетривиальность как исследования, так и полученных результатов, их новизна и математическая привлекательность для учащихся.

Конечно, в планиметрии это прежде всего задачи, явно или неявно связанные с движением.

Прежде всего, это "прямые" задачи на движения - на поворот и сдвиг, скользящий сдвиг и т.п.
Затем - задачи на максимум и минимум (здесь движение иллюстрирует постановку задачи, и помогает войти в нее).
И наконец, задачи, в которые движение входит в условие, в явной или неявной форме.

Задачи на движения, глубоко связанные с пониманием геометрии как изучения инвариантов соответствующих групп преобразований, по Клейну, связаны с классификациями замощений и с другими красивыми геометрическими объектами. К сожалению, пока математическая культура школьников не подразумевает навыка работы даже с элементарными понятиями теории групп. Несмотря на появление методических работ (см.), где предлагается использовать теоретико-групповой подход прямо в существующем курсе геометрии, и показана эффективность введения конкретных понятий (деления задач на аффинные, проективные и т.д.), пока рано говорить о введении этой темы. Тем не менее, некоторый готовый материал по этой теме, который можно использовать, можно найти на CD-диске [1].

Планиметрические задачи: источники тем и моделей.

Здесь мы отвели места представлению планиметрических моделей относительно небольшое, по сравнению с их местом и важностью в курсе. Объясняется это тем, что задачи: удобные для моделирования, и даже методики моделирования, и , наконец, сами модели опубликованы с подробными методическими указаниями и комментариями.

Прежде укажем на модели для той же среды моделирования, т.е. для Geometer's SketchPad. Прежде всего это CD-диск [1]. Школьная и внешкольная планиметрия с различными методиками работы с моделями представлены там достаточно широко. Автору принадлежат на этом диске ряд материалов, связанных с планиметрией.

Несколько сотен моделей, большая часть из которых также снабжена методическими указаниями, может быть найдена на CD-диске [2]. Автору там также принадлежат несколько десятков планиметрических моделей, с краткими комментариями.

Большое количество моделей и методических разработак выложено на англоязычных Интернет-сайтах (http://www.keypress.com) и на сайтах Европы, Южной Америки и Азии.

Большое количесство моделей и методик разработано и для близких сред моделирования, прежде всего для Cabri - французской среды для виртуального учебного моделирования (http://www.cabri.com).Задач, которые легко могут быть использованы в курсе моделирования, много. Прежде всего их можно найти в журнале «Квант» (http://www.mccme.ru), в газете «Математика» издательского дома «Первое сентября» и т.д. Задачи на максимум и минимум в планиметрии, подробно рассмотренные в классической уже книге (Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом. Геометрические неравенства и задачи на максимум и минимум. Серия: Библиотека математического кружка, вып.12 М. Наука 1970г.). Мы также использовали сборники замечательных задач с решениями и комментариями (Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом Избранные задачи и теоремы элементарной математики. Геометрия. Стереометрия.Издательство: Издательство Физико-математической литературы, 2000 г.) и (В. В. Прасолов Задачи по планиметрии МЦНМО, М.,2001)

Обратим особое внимание на публикацию (А.Я.Цукарь 7-8-9), где такжепомещено много таких задач. Они подобраны по уровню сложности, снабжены методическими комментариями и развернутыми решениями, и самое главное для нас - взяты именно в качестве задач на исследование с применением движения как эвристического метода при их решении.

Под задачами с движением в условии подразумеваются задачи, где какой-либо параметр пробегает геометрически заданную область значений, и для всего соответствующего множества конфигураций делается некоторое утверждение.

Таких задач в планиметрии много, но для курса мы выбрали самые выразительные из них, не входящие в обычный школьный курс, но упоминаемые в курсе геометрии профильного класса, и удовлетворяющие критериям, приведенным выше.

Экспериментальное определение оптимальной формы многоугольника (задача Зенодора).

Исторические сведения и введение в постановку задачи.

Эта работа непосредственно связана с идеями Зенодора.

А именно, мы проведем лабораторную работу, в которой будут эмпирически (на опыте) проверены утверждения:

Из всех многоугольников данного периметра с данным числом сторон наибольшую площадь имеет правильный многоугольник.
Среди правильных многоугольников одинакового периметра наибольшую площадь имеет тот, у которого наибольшее число сторон.
Площадь правильных многоугольников одинакового периметра при росте числа сторон стремится к площади окружности с той же длиной, что и их периметры.

Сравним эти утверждения с утверждениями древнегреческого математика Зенодора (II-I вв. до н.э.). Зенодор утверждал, что:

1) из всех многоугольников с равным периметром и равным числом сторон наибольшую площадь имеет правильный многоугольник;

2) из двух правильных многоугольников с равным периметром большую площадь имеет тот, у которого число углов больше;

3) из всех плоских фигур с равным периметром наибольшую площадь имеет круг.

Мы видим, что только второе утверждение Зенодора будет проверено в его формулировке, для первого и третьего будут проверены их частные случаи.

Этапы работы над моделью многоугольника.

Получение случайного набора точек и построение по ним «запутанного» многоугольника - невыпуклого, с самопересечениями.
«Распутывание» многоугольника - путем передвижения вершин превращаем его в выпуклый многоугольник.
Построение безразмерного отношения, измеряющего «отклонение от круглости» полученной фигуры.
Оптимизация многоугольника - путем передвижения вершин подбираем фигуру с экстремальным значением «меры круглости».
Исследование полученных значений.

Получение случайного набора точек и построение по ним «запутанного» многоугольника.

Получить случайный набор точек можно многими способами. Опишем два из них, наиболее часто применявшихся нами.

1/ Для учащихся, нуждающихся в повторении типовых объектных методов работы, принятых в ОС с графическим интерфейсом.

Первый способ:

Заполняем весь экран вручную точками, в любом порядке.
1. Вырезаем «лишние» прямоугольные области - «края» множества точек.

Второй способ:

1. Ставим вручную нужное количество точек в 2-3 ряда, для удобства счета.

Выделяем точки и включаем анимацию (по умолчанию для свободных точек она случайная)

Анимация, рандомизирующая расположение точек.

Пояснение. При получении набора точек для "запутанного" многоугольника, то есть нерегулярного многоугольника с большим количеством самопересечений можно использовать рандомизацию -

все точки выделяются и включается команда "анимация" меню "вид". Свободные точки в этом случае по умолчанию движутся по

случайным независимым траекториям, что и позволяет получить нужный результат.

Теперь можно применить инструмент «Гомотетия» - и движеним мышки выбрать удобный масштаб - так, чтобы точки и не выходили за границы экрана, и не теснились в его центре.

«Распутывание» многоугольника - путем передвижения вершин превращаем его в выпуклый многоугольник.

Теперь можно поставить задачу «распутать» полученный многоугольник, то есть двигая мышкой его вершины, превратить его в многоугольник без самопересечений, и в конце концов - в выпуклый.

Разница между динамическим и статическим решением.

Здесь важно уточнить задачу, так как разницу между рисунком и динамическим чертежом не все учащиеся могут чувствовать. Если они понимают чертеж как рисунок, ничто не мешает, совмещая вершины, «прятать щели» внутри фигуры, что, конечно, не решает задачу - «малое шевеление» разрушает видимую целостность фигуры.

Формирование системности в поисковой деятельности

Если точек немного, можно и беспорядочными («поисковыми») движениями решить задачу. Если их больше двадцати - бессистемное распутывание, как и при распутывании настоящих клубков ниток, проволоки или лески, никакого эффекта не даст (кроме обратного). Здесь нужно нащупать метод распутывания, и последовательно его довести до конца.

Поэтому так важно выбрать меру сложности задачи точно для данного класса - чтобы трудности решения не подавляли, и путь решения был найден самостоятельно.

Пример метода решения задачи для большого числа точек

Один из самых простых методов решения приведен на чертеже. Он состоит в том, чтобы, пошевелив мышкой очередную точку, замечать, какая будет следующая (по выбранному направлению обхода - например, по часовой стрелке - и ставить их вне узла одну за другой, пока не обращая внимания на остальные точки.

1. 2.

3. 4,

Алгоритм «распутывания» многоугольника с самопересечениями.

Пояснение. На рисунке (1.) показан исходный "запутанный" многоугольник. На втором рисунке (2.) - результат применения алгоритма "распутывания" - по воображаемой линии, окружающей многоугольник, последовательно

выстраиваются (перетаскиваются мышкой) точки, являющиеся последовательными вершинами многоугольника в выбранном направлении обхода. Выбор первой точки и направления обхода не влияет на результат. Очередную точку помогает определить простой прием -

"малое шевеление" предыдущей точки. При этом "зашевелятся" и примыкающие к ней две стороны. Останется выбрать одну из двух точек, на которые укажут эти стороны. Выбор определяется направлением обхода.

Ход «распутывания» многоугольника.

Эта простейшая топологическая задача также имеет интересное развитие. К близкому классу задач («на распутывание») учащиеся вернуться после вводных занятий. (см. Нечисловая оптимизация)

Построение меры «отклонения от круглости».

Следующий этап - построение «меры круглости» фигуры. Он восходит к древней «задаче царицы Дидоны».

Этот тип задач также может быть рассмотрен подробнее. (см. пункт «Задача царицы Дидоны (изопериметрические задачи)».

Этот этап удобно проводить в форме групповой работы, возможно, и фронтальной. Все возникающие предложения по построению «меры круглости» можно тут же записывать в рабочем поле (оно должно отображаться либо на общем экране, либо на экранах всех компьютеров учеников). Затем проводится эксперимент- изменяется масштаб фигуры. Выражения, реагирующие на изменение масштаба, удаляем. Оставить можно любое удачное выражение, только нужно обратить внимание на количество десятичных знаков - значащих цифр должно быть не меньше трех-четырех (для возможности сравнивать соревнующихся). Последнее из выражений на рисунке - отношение площади к квадрату периметра - как раз нуждается из-за этого в увеличении точности (через меню «свойства»).

Пример чертежа при коллективной работе над гипотезой.

Пояснение. На чертеже выписываются все предложенные учащимися выражения, а затем происходит их экспериментальная проверка - всех сразу - с помощью гомотетии многоугольника. Принцип проверки прост - при гомотетии многоугольника некоторые выражения не изменяются, но при изменении его формы меняют значение. Щелкнув инструментом "гомотетия" на любой точке внутри многоугольника, "тащим" эту (или другую) точку. При этом часть выражений меняет свое значение - значит, они не выдержали проверки. Затем "тащим" многоугольник за вершину (инструментом "указатель") - и теперь все "правильные" выражения должны, напротив, поменять свои значения.

Оптимизация многоугольника.

Путем передвижения вершин подбираем фигуру с экстремальным значением «меры круглости»

Пример начального положения модели для ручной оптимизации безразмерного отношения - меры «круглости» фигуры (точность - четыре значащие цифры.)

Пояснение. Наш объект - "вычисление", т.е. найденное динамическое выражение. В контекстном меню, возникающем, как это уже привычно, при щелчке правой кнопкой мыши на нужном объекте, выбор строки "свойства" удобен для изменения параметра "точность".

Берем предельную точность "стотысячные". Это дает нам - предел для ручной манипулятивной работы на стандартном экране.

Виды возможных подсказок - «каркасов» для ручной оптимизации фигуры - окружность, звезда, обод.

Пояснение. При манипулятивной работе по подбору оптимальной формы хорошо использовать "подсказки" - дополнительные построения, помогающие ручному манипулированию. Первый рисунок - просто окружность, которую расположить лучше так, чтобы задаваемая ей коррекция фигуры была минимальна. Все вершины нужно поставить на эту окружность, по возможности равномерно. Второй рисунок - вырожденная "правильная звезда", количество лучей которой совпадает с количеством вершин фигуры. Вершины нужно расположить на этих лучах, по возможности на равных расстояниях от центра. И наконец, можно объединить две подсказки - точки пересечения окружности и «звезды» указывают уже точное положение вершин для правильного многоугольника.

Один из учеников СУНЦ догадался облегчить свою работу, начертив рядом с многоугольником окружность, и подтащив вручную к ней вершины. Эта идея получила некоторое развитие - мы используем и альтернативную подсказку - звезду из N лучей, где N - число вершин многоугольника. Предлагая учащимся, по сути, решать задачу вручную, но при ограничениях на форму многоугольников, мы получаем возможность дать почувствовать, как при этом увеличивается точность решения. Наконец, если мы доведем ограничения до предела, совместив обе подсказки, то получим единственное (с точностью до гомотетии и вращения) решение - правильный N - угольник.

Методические детали работы с точностью.

При этом точность обычно еще возрастает - хотя бы на десятую или несколько сотых процента, что обычно впечатляет учащихся, бившихся за каждый знак и все равно, как оказывается, не добившихся вручную оптимальной конфигурации (чисто вручную точный правильный многоугольник построить тяжело, даже имея критерий в виде соответствующего отношения).

Пример наилучшего значения, полученного при использовании подсказки - вершин правильного многоугольника

Пояснение. Пример применения "подсказки" - точки подтянуты к вершинам правильного многоугольника. Это можно сделать как вручную, так и автоматически, по команде "совместить точки" из меню "правка" (точки нужно выделить). Это значение должно совпасть с полученным теоретически (упражнение для тех, кто успел все построить раньше других).

Исследование полученных значений.

Конечно, при ручной оптимизации учащиеся или спрашивают, или, не дожидаясь ответа, сами вычисляют - «а какое же наилучшее значение?». На этот вопрос отвечает простая модификация модели - вместо N - угольника берем окружность, которую можно рассматривать как «очень-много-угольник», делаем измерения (вместо периметра берем уже длину окружности) и вычисляем нужное отношение. Его легко получить и аналитически.

Экспериментальное и аналитическое получение верхней границы отношения S/(P*P) для правильных многоугольников через аналогичный расчет для круга.

Пояснение. При увеличении числа сторон многоугольник приближается к кругу, и в соответствующих отношениях вместо периметра будет длина окружности, а вместо площади многоугольника - площадь круга. Это отношение нетрудно вычислить теоретически, и его значение, как видно на чертеже, совпадает с полученным экспериментально.

Довольно быстро учащиеся замечают, что лучшие результаты у тех, у кого число вершин больше, даже если их оптимизация более грубая.

Здесь можно вернуться к формулировкам Зенодора, или сказать о том, что подробное рассмотрение этих вопросов - одна из следующих тем, а именно тема «Теорема Гюйгенса об оценке числа «пи»» . Тем не менее и это занятие дает опыт встречи с понятием предела - фактически мы рассматриваем окружность как предел последовательности правильных многоугольников.

Задача царицы Дидоны (изопериметрические задачи).

Геометрические задачи, в которых отыскивается фигура с экстремальным свойством среди других фигур с равным периметром, называются изопериметрическими.

Это классическая экстремальная задача, о важности которых замечательно сказал П.Л.Чебышев: «Среди огромного количества задач, которые ставит перед человеком его практическая деятельность, особенную важность имеет одна: «Как располагать средствами своими для достижения по возможности большей выгоды». Именно поэтому «большая часть вопросов практики приводится к задачам наибольших и наименьших величин, совершенно новым для науки, и только решением этих задач мы можем удовлетворить требования практики, которая везде ищет самого лучшего, самого выгодного».

Напомним, что в математике решения задачи на экстремум понимают так: дать ответ и доказать его экстремальное свойство.

Задачи моделирования - другие, соответственно изменяется и ход работы. Сначала надо изучить на построенных для этого моделях поведение фигуры, сделать предположения о значениях экстремума, найти их с нужной точностью, и приготовиться к доказательству, проверив численно максимально широкий круг параметров.

На задаче Дидоны мы проследим все указанные этапы.

Теоремы Зенодора.

Изопериметрические задачи рассматривал древнегреческий математик Зенодор (II-I вв. до н.э.). Именно Зенодор утверждал, что:

3) из всех плоских фигур с равным периметром наибольшую площадь имеет круг.

Строгое доказательство третьего утверждения Зенодора было доказано только в XVIII веке знаменитым математиком Л. Эйлером.

Изопериметрические задачи известны также под названием “задачи Дидоны” по имени легендарной основательницы города Карфагена и его первой царицы. Согласно легенде, вынужденная бежать из своего родного города, Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей место для нового поселения. Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитроумная Дидона разрезала воловью шкуру на узенькие ремешки и, разложив их, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было бы покрыть шкурой целиком. Если учесть, что Дидона выбирала участок, примыкающий к берегу морю, то на языке математике задачу, стоящую перед Дидоной можно сформулировать так: какой формы должна быть кривая длины l, чтобы площадь фигуры, ограниченная этой кривой и заданной линией Г, была наибольшей.

Можно решить задачу Дидоны в нескольких частных случаях: если береговая линия - прямая и ограниченный воловьими ремешками участок - прямоугольник, или четырехугольник, или пятиугольник и т.п..

Мы дадим пример работы в случае прямоугольника.

Сначала строим модель для экспериментального решения. В ней прямоугольник должен иметь возможность так изменяться, чтобы пробегать все возможные значения, и при этом можно было бы следить за площадью. Построить такую фигуру нетрудно.

Три стороны прямоугольника - ломаная постоянной длины, отгораживающая максимальную площадь.

Пояснение. Динамический чертеж иллюстрирует задачу Дидоны в случае, если береговая линия - прямая, а участок, ограниченный воловьими ремешками - прямоугольник. На компьютерном чертеже точка С двигалась снизу вверх, и все стороны огороженного участка при этом оставляли следы. Виден след АВ и ВС, след же отрезка СD при таком движении "затирается" следом отрезка ВС.

Теперь останется поместить на чертеж соответствующие динамические измерения, и можно проводить эксперимент по определению наилучшей формы.

Решим эту же задачу алгебраически. Вот пример решения:

Пусть l- длина воловьих ремешков, x - меньшая сторона прямоугольника, тогда (L-2x) - большая его сторона.

Площадь S будет равна x(L-2x). Максимум квадратичной функции достигается при значении переменной, равном абсциссе вершины параболы. Но этот кажущийся очевидным геометрический факт тоже требует доказательства - математики не должны доверять очевидности.

В алгебре это обычно доказывается разложением квадратного трехчлена в полный квадрат и рассмотрением получившейся суммы.

-2x2+Lx=-2(x-L/2)2+L2/2

Из этого выражения видно, что максимум достигается при x=L/2, он единственен и равен L2/2.

Второй пример - равнобедренный треугольник (на самом деле требование равнобедренности излишнее, но оно упрощает задачу). Эксперимент показывает, что максимум достигается при угле в 90 градусов.

Равные стороны равнобедренного треугольника - ломаная постоянной длины, отгораживающая максимальную площадь.

Пояснение. Иллюстрация, аналогичная предыдущей, в случае замены четырехугольника на равнобедренный треугольник; но точка С здесь движется сверху вниз. Чертеж иллюстрирует задачу Дидоны в случае, если береговая линия - прямая, а участок, ограниченный воловьими ремешками - равнобедренный треугольник.

Теперь, наконец, нетрудно заметить, что и в первом, и во втором случае оптимальная фигура - половинка квадрата. Это приводит к мысли достроить вторую половину:

Пояснение. Если отразить наилучшие траектории для двух рассмотренных случаев относительно береговой линии, в обоих случаях получим квадрат. Это может навести на мысль о простом доказательстве полученных гипотез, если знать оптимальные свойства квадрата для задачи Зенодора в случаях прямоугольника и ромба.

Глядя на этот чертеж, легко уже заметить, что он как раз служит доказательным чертежом в духе древнеиндийского принципа («смотри!»). У фигуры, полученной объединением начальной и отраженной, периметр постоянный, так как он ровно в два раза больше суммы длин ломаных. Поскольку и у ромба, и у прямоугольника постоянного периметра площадь максимальна, когда это квадрат (по теореме Зенодора о правильных многоугольниках), то оптимальная фигура и в том и в другом случае - половина квадрата. Этот результат легко распространяется учащимися на ломаную с любым количеством звеньев.

Задача на максимум площади параллелограмма, вписанного в треугольник.

Постановка задачи.

Пусть в треугольник вписан параллелограмм таким образом: на одной из сторон ставится точка, из нее проводятся параллельные двум остальным сторонам. Считается (измеряется) площадь получившегося параллелограмма. Где нужно выбрать точку на данной стороне, чтобы площадь его была максимальна?

Пояснение. В этой модели две стороны параллелограмма всегда лежат на сторонах треугольника, а точка К движется по стороне АВ. Построив динамическое измерение площади параллелограмма, экспериментально определим положение точки К, при котором эта площадь максимальна.

Предположение подкрепим измерением, а затем и доказательством, которое здесь несложно.

График изменения площади параллелограмма в зависимости от положения точки К.

Эта задача - не изопериметрическая

Заметим, что для неравнобедренных треугольников периметр параллелограмма LKDC не является постоянным, он линейно изменяется от удвоенной величины одной стороны до удвоенной величины другой, и поэтому назвать последнюю задачу изопериметрической уже нельзя.

Для равнобедренных же треугольников доказательство соответствующего утверждения теоремы Зенодора совсем несложно, и также может быть проиллюстрировано на динамическом чертеже.

Такую иллюстрацию можно подготовить или самому преподавателю, или поручить подготовить учащемуся, закончившего курс. Дело в том, что эффективность таких чертежей для математических целей (в данном случае - помощь в понимании смысла теоремы и её доказательства) достаточна, но для целей вводного курса моделирования они слишком близки к обычным чертежам из учебника геометрии, и не лежат на той границе известного и неизвестного, которая увлекает большинство учащихся.

Иллюстрация теоремы Зенодора для изопериметрических параллелограммов с фиксированным углом.

Пояснение. Максимальную площадь среди них имеет ромб. Доказательство следует из того, что площадь ABCD всегда меньше (или равна) площади AGEH, так как у этих параллелограммов с равными углами две стороны равны, а сумма двух других постоянна.

Прямая Симпсона и ее связь с треугольником Морли.

Эти работы, проводимые синхронно с уроком геометрии, касающимся тех же тем (руководитель - к.ф.м.н. В.Н.Дубровский) предложены для данного курса преподавателем кафедры математики СУНЦ к.ф.м.н. Ю.Е.Егоровым.

Поддержка курса геометрии в курсе моделирования - опыт взаимодействия.

Следующие лабораторные работы по темам «Прямая Симпсона…», «Теорема Понселе», результат прямого взаимодействия преподавателей математики и информатики. В 10-м классе СУНЦ в курсе геометрии есть ряд тем, которые для лучшего усвоения нуждаются в компьютерной поддержке. С другой стороны, компьютер позволяет сделать «шаг за границы школьной программы», познакомив учащихся с удивительными фактами, касающимися только что пройденного материала. Важно подчеркнуть именно факт готовности учащихся воспринять новый факт, удивиться ему, задать себе вопрос - а как же это возможно, почему так? Если такое удивление возникает, то важно дать возможность школьникам сделать несколько шагов в исследовании, даже если эти шаги не могут всех привести к полному и точному ответу. Именно здесь математическое моделирование дает возможность подготовить «педагогический прорыв» - ученик может сделать те несколько самостоятельных шагов, важность которых нельзя переоценить в становлении человека. С другой стороны, методические усилия учителя информатики должны быть направлены на то, чтобы создать баланс между трудностью самостоятельного построения модели и субъективной важностью её для учащегося. В случае взаимодействия учителя математики и учителя информатики сделать это проще, так как «зона ближайшего развития» подготавливается одновременно (и согласованно) преподавателями двух предметов, а значит, может возникнуть дидактическая взаимоподдержка по затрагиваемой теме (и она действительно возникает, см. ()).

Краткое описание хода лабораторной работы.

Построим прямую Симпсона для треугольника АВС и точки Е на описанной вокруг треугольника АВС окружности О.

Затем построим геометрическое место точек , заметаемое этой прямой при движении точки Е по окружности О.

Получим фигуру, называемую «дельтоида Штейнера». Соединим вершины фигуры отрезками. Получим треугольник КМР.

Теперь построим инструмент трисекции угла (разумеется, приближенный). С помощью него построим для треугольника АВС треугольник Морли.

Задание - подобрать центр и коэффициент гомотетии, переводящей треугольник Морли для треугольника АВС в треугольник КМР, построенный на дельтоиде Штейнера для треугольника АВС.

По результату сформулировать гипотезу.

Методические особенности работы.

Заметим, что дельтоиду многие учащиеся получили как один из результатов работы спирографа. Спирограф же они построили, выполняя самостоятельную работу по теме “Механизм Витгенштейна”. Известно, что если радиус внутренней окружности спир0ографа меньше радиуса большой окружности в три раза, то точка опишет кривую Штейнера (дельтоиду). Приведен пример такой работы.

Дельтоида, как один из предельных циклов спирографа.

Пояснение. Дельтоида часто возникает в различных геометрических задачах. Например, этот чертеж был получен как один из результатов работы спирографа, построенного учащимся 10-в класса СУНЦ Олегом Баскаковым в 2005 году «между делом», в качестве любопытного мини-проекта.

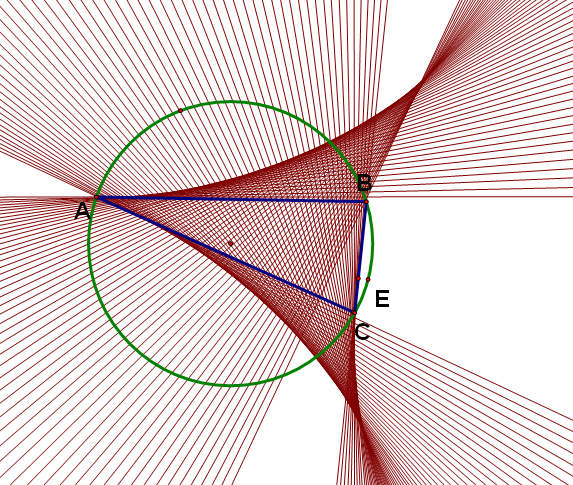
Дельтоида Штейнера, как ГМТ прямой Симпсона, и треугольник Морли (на пересечениях трисектрис).

Пояснение. Прямая Симпсона проходит через основания высот, опущенных на стороны треугольника из точки на описанной вокруг него окружности.

На чертеже построено геометрическое место точек прямой Симпсона при всех возможных положениях точки на описанной окружности.

Треугольник Морли получается при пересечении трисектрис, т.е. лучей, делящих угол на три равные части. Он всегда равносторонний.

Треугольник, построенный на вершинах дельтоиды Штейнера, гомотетичен треугольнику Морли.

Пояснение. На чертеже для исходного треугольника АВС построено ГМТ прямой Симпсона и треугольник Морли. При движении исходной точки по описанной окружности прямая Симпсона описывает дельтоиду Штейнера. Вокруг дельтоиды Штейнера описан треугольник. Видно, что стороны полученного треугольника параллельны сторонам треугольника Морли. Это значит, что они гомотетичны.

Теорема Понселе.

В журнале "Квант" (2003,N3, Заславскй А., Косов Д., Музафаров М., Траектории замечательных точек треугольника Понселе) опубликовано доказательство теоремы Понселе и ряда связанных с ней утверждений, доступное учащимся профильных классов. Эта замечательная теорема содержит движение фигуры в своей формулировке, причем движение именно того типа, который и воспроизводится средой Geometer's SketchPad (Живая Математика).

Экпериментальная установка по изучению треугольников Понселе.

Пояснение. Чертеж ученика 10-в класса СУНЦ Струкова (2005 г.).Вокруг исходного треугольника описана окружность, внутри него - вписанная окружность. Тогда, если две точки треугольника лежат на описанной окружности, а вписана в тругольник та же окружность, то и третья

точка будет лежать на описанной окружности. Таким образом строится непрерывное семейство треугольников, описанных вокруг этой окружности. Это семейство изображено на чертеже как след движущегося треугольника.

Факт, обнаруженный Струковым на построенной им установке, таков: след, оставляемый всеми серединами средних линий треугольников Понселе, один и тот же.

Модель к теореме Понселе: движение точки по описанной окружности заставляет двигаться всю фигуру вокруг вписанной окружности.

Пояснение. Если из исходной точки на внешней окружности выпустить луч, касающийся внутренней окружности, и из точки пересечения этого луча с внешней окружностью снова выпустить луч таким же образом, для получения второго звена ломаной, то может случиться так, что ломаная на N-ом шаге замкнется. Тогда замкнется на том же шаге и любая другая ломаная, построенная по этому алгоритму, но из другой исходной точки на внешней окружности.

Об одном способе уточнении оценки числа «пи» (Гюйгенс)

Цель работы - освоение методики уточнения оценок путем взвешенной интерполяции и обнаружения возможности такого уточнения и закрепление понятий «точность оценки», «порядок точности оценки», «сравнение оценок».

Краткое содержание работы

Эта работа проводится на модели правильного многоугольника, вписанного в окружность и описанного вокруг нее же. По каждому многоугольнику строится приближение числа «пи» - соответственно, «сверху» и «снизу».

По таблице точности приближений должна быть (желательно самостоятельно) замечена закономерность, впервые обнаруженная Х.Гюйгенсом: систематичность ошибок, заключенная в том, что точное значение всегда очень близко к точке первой трети интервала между оценками «сверху» и «снизу».

Таким образом, можно уточнить оценку, беря за приближение значение, полученное из двух оценок путем взвешенной интерполяции с коэффициентом 1/3.

Возможное углубление задачи.

Этот факт получается как чисто экспериментальный, но в качестве задачи для желающих можно предложить сравнить точность полученной оценки и исходных - например, путем разложения их в ряд Тейлора и оценки остаточного члена (в СУНЦ эти темы входят в программу по математике).

Для этого можно включить занятие по экспериментальному построению полиномиального разложения необходимых функций - синуса и тангенса - в окрестности нуля (т.е. отрезка ряда Тейлора), которое будет описано ниже.

Основные этапы работы

Строим движок для переменной - количества сторон многоугольника, сторону вписанного правильного многоугольника, затем сторону описанного многоугольника.

Строим динамический правильный многоугольник, первый шаг - построение динамического сектора и сегмента.

Пояснение. АВ - движок, т.е. отрезок, изменяя который, мы изменяем его длину. По длине рассчитывается количество сторон, а по нему - угол правильного многоугольника. Поворачивая радиус на этот угол (командой «повернуть» меню «преобразование»), мы можем построить стороны правильных многоугольников - вписанного и описанного вокруг данной окружности.

2. Строим с помощью команды «Итерация» правильные многоугольники с переменным количеством сторон - вписанный и описанный, измеряем их стороны и вычисляем их периметры. Строим оценку числа «Пи» - отношения периметров к диаметру окружности, заполняем таблицу и по таблице строим график в прямоугольных координатах (для простоты масштабирования).

Второй шаг построения модели построение вписанного и описанного многоугольника (с помощью команды «итерация»).

Пояснение. Изменяя движком количество сторон, заполняем таблицу (для этого достаточно щелкнуть на ней мышью). По заполненной таблице строим график сходимости оценок числа «пи».

3. По графику можно сделать экспериментальный вывод о сходимости верхней и нижней оценки к числу «пи» и предположение о расположении числа «пи» в интервале между верхней и нижней оценкой. Предположение можно проверить на нескольких табличных значениях. Далее необходимо обосновать переход к безразмерной (нормированной) форме представления результатов эксперимента. При этом нужно ясно сформулировать ее преимущества относительно графической и табличной формы. И наконец, строится улучшенная оценка числа «пи» - как взвешенное арифметическое среднее верхней и нижней оценки с коэффициентом 1/3.

Третий шаг построения модели - построение новой оценки числа «пи» на основе полученных.

Пояснение. Динамический чертеж при изменении числа сторон многоугольника (при помощи мышки, которой ухватываемся за правый конец движка и тащим его) позволяет проследить положение точного значения числа «пи» на «обезразмеренной» шкале - и оно оказывается всегда близко к 1/3.

Теперь мы можем повторить предложение Х.Гюйгенса в качестве приближения использовать эту точку обезразмеренной шкалы. Соответствующий пересчет в абсолютную шкалу дает взвешенное значение в качестве результата.

4. По результатам эксперимента обсуждаются особенности сходимости полученных трех оценок, и пути доказательства обнаруженных их свойств.

Для этого строится таблица, в которой собраны данные о точности оценок в связи с ростом числа сторон многоугольника. Из таблицы можно увидеть, что порядок убывания ошибок у оценки Гюйгенса более высокий, чем порядок убывания двух исходных оценок.

Четвертый шаг - это просто уточнение третьего.

Пояснение. По построенной на третьем шаге модели на том же чертеже строится таблица для оценки порядка сходимости всех трех оценок - двух старых оценок и новой оценки. По таблице также можно построить график, но на графике постоянного масштаба порядок здесь трудно исследовать, а графики переменного масштаба мы пока не включили в программу курса.

План доказательства улучшения взвешенной оценки.

Путь доказательства улучшения оценок может быть таким, например:

Разложим обе исходные оценки в ряд Тейлора в окрестности нуля.

Они сведутся соответственно к оценке синуса и тангенса переменного угла.

Если мы из них составим взвешенную оценку, то увидим, как при этом неточности оценок скомпенсируются:

Этот прием повышения порядка сходимости может быть распространен и на другие задачи уточнения оценок. Например, сходным образом устроена квадратура Симпсона.

Алгебра и анализ.

Экспериментальное построение многочлена для приближения функции.

Данная работа может включаться в курс как подготовительная для работы с оценкой Гюйгенса.

Для лучшего понимания факта, открытого Гюйгенсом, полезно познакомиться с теоретическими объяснениями. Для этого, в свою очередь, может послужить занятие по экспериментальному построению полиномиального разложения необходимых функций. А именно, потребуются разложения синуса и тангенса в окрестности нуля (т.е. отрезки ряда Тейлора).

В силу особого пропедевтического значения этой работы мы приведем ее краткое описание с необходимыми комментариями.

Методическое соотношение с соответствующим разделом математического анализа.

Методическая особенность этой работы состоит в том, что она не должна создавать у учащихся впечатления, что они познакомились с соответствующим разделом анализа - разложением в ряд Тейлора. Мы обычно даже не упоминаем о том, что это разложение близко к ряду Тейлора для данной функции.

С другой стороны, важность затрагиваемого в работе круга понятий (прежде всего понятий приближения и порядка точности приближения) для математического моделирования такова, что не коснуться их совсем было бы тоже неверно.

Выход, который мы здесь предлагаем, заключается в сужении задачи до прагматической - приближении именно синуса и именно тангенса, без теоретических обобщений, по простейшему методу.

Ход работы.

Организация работы

На первом этапе, этапе напоминания теоретического материала и постановки задачи, удобно использовать проектор (или интерактивную классную доску), который дает возможность привязать пояснения к зрительному образу, причем, как и на доске, нужно располагать материал так, чтобы следы всех этапов работы на ней оставались. Конечно, на экране это сделать легче, так как можно просто любую часть изображения передвинуть в любое место, организуя одновременно и пространство работы, и пространство «следов» работы.

Дальше можно двигаться по двум путям - или раздать учащимся листочки, содержащие последнее состояние экрана с минимальными пояснениями (тогда проектор можно отключить), или оставить проектор включенным, с тем, чтобы учащиеся могли посмотреть на экран при затруднениях.

Этапы работы

Вводное пояснение о смысле получения приближения функции многочленом в окрестности некоторой точки. Выбор конкретной функции и точки. Демонстрация идеи получения приближения. Закрепление понимания содержания шага приближения. Уточнение понятий и обобщение результатов.

Постановка задачи: самостоятельное получение приближения многочленом той же степени, для той же (или другой) точки, для другой (или той же) функции, анализ точности.

Выяснение смысла слов «приближение многочленом»

Прежде всего необходимо понять, что значит «получить приближение» - в каком именно смысле многочлен является приближением в окрестности нуля?

Самый простой - это такой многочлен, у которого наименьшая ошибка приближения среди всех других многочленов. При этом мы рассматриваем только многочлены определенной степени, обычно не выше седьмой. За ошибку приближения в нуле возьмем максимум модуля разности между синусом и многочленом в данной окрестности, или максимальное расхождение между функцией и приближением.

Тогда лучшим многочленом нулевого порядка будет нуль, потому что синус - нечетная функция, и в нуле равен нулю.

Точность этого приближения в окрестности нуля мы можем оценить так: какова окрестность нуля, в которой точность нашего приближения будет лучше 1% ? Это сделать нетрудно - по графику видно, что этот интервал примерно равен [-0,01 , 0,01] . Можно построить и вполне строгую оценку, используя школьный материал - теоремы о замечательных пределах, но это снова территория преподавателя математики.

Следующий шаг - построение многочлена первой степени.

Ход построения многочленов - от первой до седьмой степени.

Основная идея - использование уже полученного приближения для построения следующего. Совсем не очевидно, что это всегда можно сделать - для равномерного приближения на отрезке, например, это не совсем так. Делать ли это замечание и приводить ли соответствующий пример (даже на уровне интуитивной понятности) - вопрос, который учитель должен решить сам для каждого конкретного случая (уровень класса, количество часов, спектр целей и т.п.).

Итак, попробуем положиться на то, что следующее приближение будет иметь ту же константу - ноль.

Это равенство - точное, при подборе соответствующей функции

Приближение будет состоять в замене этой функции на константу:

Тогда многочлены первого порядка нужно искать среди линейных функций вида

Строго говоря, для подбора b достаточно найти предел

Это один из «замечательных пределов», он равен единице.

Но мы будем искать его экспериментальным путем - рассматривая график функции

Чтобы повысить точность определения координат, поместим на чертеж точку А, у которой измерим ее координаты. Совместив точку А с точкой на графике, мы сможем получить координаты с большей точностью, чем по шкале на оси ординат (абсцисса нам в данном случае не нужна).

Таким образом, мы нашли два приближения

sin(x) = 0 +…

sin(x) = x + …

Подбор второго коэффициента для многочлена, приближающего синус.

Пояснение. Первый коэффициент - при единице - равен нулю. Чтобы найти второй, ищем значение отношения разности синуса и предыдущего приближения к х.

Оценим точность второго полученного приближения. Для этого удобно подвигать пробную точку по графику нормированного модуля разности между приближением и приближаемой функцией. Тогда сразу можно оценить границы интервала, в котором эта разность между функцией и её приближением не выходит за границы 1% .

Экспериментальная оценка относительной погрешности полученного приближения.

Пояснение. На этом чертеже мы строим график относительной погрешности полученного приближения в окрестности нуля. Экспериментальным путем находим границы интервала вокруг нуля, в котором эта погрешность меньше 1%. Но масштаб графика не очень удобен для такого поиска. Для повышения точности применяем обычный прием - создаем свободную точку, измеряем ее координаты, и помещаем в различные точки графика (по аналогии с пробным зарядом).

Из графика видно, что это интервал [-0,24 , 0,24], то есть интервал приближения с точностью 1% стал шире, чем был на первом шаге.

Чтобы найти приближение следующим многочленом, квадратичным, снова выпишем функцию, дающую значение ошибки, и построим ее график.

sin(x) = x+c(x)x2

Найдем приближение квадратичной функцией, точно так же заменив с(x) подходящей константой. Найти эту константу мы можем графически.

Подбор третьего коэффициента для многочлена, приближающего синус.

Пояснение. Первый коэффициент - при единице - равен нулю, второй - при х - равен единице. Чтобы найти третий, ищем значение отношения разности синуса и предыдущего приближения квадрату х. Это отношение, как видно из получающегося при разных масштабах графика, с большой точностью равно нулю.

С высокой точностью это ноль.

Ищем кубический многочлен:

Построив график функции с(x) , заменим ее на постоянную в точке приближения, то есть в нуле. По графику видно, что это около -0,1666… Переходя к обыкновенным дробям, получим -1/6. Заметим, что 6=3!=1*2*3.

Повторяя этот процесс для четвертой степени, снова получим очень близкую к 0 величину, как и для второй степени.

Первый чертеж посвящен подбору коэффициента для кубического члена приближения, а второй - для члена четвертой степени.

Пояснение. Первый коэффициент - при единице - равен нулю, второй - при х - равен единице, третий -снова нуль. Чтобы найти четвертый, ищем значение отношения разности синуса и предыдущего приближения к кубу х.

Это отношение, как видно из получающегося графика, примерно равно одной шестой. Та же схема для следующего коэффициента дает снова нуль (на втором чертеже).

Оценим точность этого нового приближения. Опять подвигаем пробную точку по графику нормированного модуля разности между приближением и приближаемой функцией и оценим границы интервала, в котором эта разность между функцией и её приближением не выходит за границы 1% .

Механическое моделирование в работах П.Л.Чебышева

С именем замечательного русского математика 19-го столетия Пафнутия Львовича Чебышева связаны приложения математики к механике. Интересно, что Пафнутий Львович сам вытачивал на станках свои шарнирные механизмы, в основном из бронзы. В Санкт-Петербурге, в музее исНа этом чертеже мы строим график относительной погрешности полученного приближения в окрестности нуля.

Пояснение. Экспериментальным путем (по графику) находим границы интервала вокруг нуля, в котором эта погрешность меньше 1%. Но масштаб графика не очень удобен для такого поиска. Для повышения точности применим масштабный множитель (100), а затем другой обычный прием - создаем свободную точку, измеряем ее координаты, и помещаем в различные точки графика (по аналогии с пробным зарядом). На этом графике относительная ошибка дается в процентах. Интервал в один процент не помещается на приведенном чертеже, поэтому придется подвинуть точку (1,0), задающую единичный отрезок для графика.

По графику определяем, что это интервал [-1,01 , 1,01], то есть интервал приближения с точностью 1% стал шире, чем был на предыдущем шаге. (Это значение на кривой в скриншот не поместилось…)

Для пятой степени получить по графику значение не сразу удается - приходится уже применять масштабные множители. Но значение определяется довольно точно - это 1/120 . Можно заметить, что 120 равно 5!=1*2*3*4*5. Интервал точности в 1% получается уже [-1,75 , 1,75]

Для шестой степени - снова ноль, для седьмой с трудом удается получить значение -1/5040 . Можно догадаться по аналогиями с предыдущими шагами, что 5040=7!=1*2*3*4*5*6*7. Интервал точности «лучше 1%» равен [-2,38 , 2,38].

Большей степени на этом пути достичь уже труднее, но и полученных значений довольно, чтобы догадаться о закономерности значений коэффициентов.

На чертеже получен коэффициент для седьмой степени.

Пояснение. Для этого пришлось применить большой масштабный множитель - 100000. Полученное при этом экспериментально значение - 1/5040.1 оказывается очень близким к 1/(2*3*4*5*6*7), так как 1*2*3*4*5*6*7=5040 Конечно, заметить это можно, только продолжая по аналогии закономерность, замеченную для третьей и пятой степеней.

Построив на графике поочередно все найденные приближения, мы видим, как многочлены постепенно приближаются (сходятся) к графику синуса. Тем не менее о сходимости мы продолжаем говорить лишь на интуитивном уровне, не вдаваясь в точные детали и определения. Можно обратить внимание и на равномерность в характере этого приближения, опять же не вводя определения равномерной сходимости. Такой опыт наблюдения математических явлений важен, как пропедевтика ключевых понятий анализа, для тех, кому предстоит их осваивать, и не перегружает тех, кто не вернется к ним.

Сводный график всех полученных приближений.

Экспериментальная оценка порядка приближения в точке.

График всех многочленов постепенно подходит к графику синуса. Но это пока - очень приблизительный, экспериментальный, чисто эмпирический факт. Поскольку приближалась функция в окрестности нуля, именно поведение приближения в окрестности нуля характеризует полученное приближение.

Сводный график для относительных ошибок с таблицей интервалов для однопроцентной ошибки.

В свою очередь, можно поставить вопрос - если сравнить поведение ошибки с окрестности нуля с поведением парабол - квадратичной, кубической и т.п., то какая именно парабола лучше всего приближает ошибку? (Правда, удобнее здесь перейти от относительной к абсолютной ошибке).

Эта задача проще уже решенных, и учащиеся без большого труда экспериментально обнаруживают, что

для r1(x) это x3 ,

для r3(x) это x5 ,

для r5(x) это x7 ,

для r7(x) это x9 и т.д.

Лабораторная установка - динамический график для подбора порядка и коэффициента абсолютной ошибки полученного приближения.

Работа учащегося 10-в класса СУНЦ (2005 г.)

Пояснение. На графике сначала проверялся одночлен восьмой степени, затем девятой и десятой. Эксперимент показал хорошее совпадение одночлена с ошибкой именно для девятой степени (он показан на рисунке - видно, что при некотором К достигается хорошее приближение).

Порядок одночлена, хорошо приближающего ошибку точности, называют «порядком погрешности в точке» выбранной оценки.

О смысле параметра «порядок точности».

Важно подчеркнуть принципиальную разницу двух параметров оценки точности - коэффициента при одночлене, и его степени. Учащиеся должны ясно понимать приоритет второго параметра для динамического поведения модели, а именно, при приближении аргумента к нулю. Приоритет в том смысле, что коэффициент определяет только масштаб приближения, сам же характер (форму графика) приближения в точке определяется степенью. Например, при квадратичном порядке коэффициент 100 уравновешивается убыванием аргумента в 10 раз, а при кубическом - убыванием меньше чем в 5 раза

Организация работы по оценке порядка точности приближения в нуле.

Можно работу по оценке порядка точности приближения провести на отдельном занятии, начать которое целесообразно с закрепления понятий, явно или неявно введенных при построении модели. Для этого можно использовать любые формы быстрого повторения, которыми владеет преподаватель.

После этого можно задать вопрос - что мы узнали о поведении ошибки вблизи нуля?

При этом удобно дать каждому проводить эксперимент с одной функцией - r1(x) или r3(x) и т.д. (на выбор), а потом объединить результаты, отсеять ошибочные и сделать общий вывод. Вывод здесь может состоять в гипотезе о связи порядка полинома, взятого для получения приближения, и порядка ошибки.

Ограниченность полученного результата и темы проектных работ.

Мы получили наилучшее приближение «в точке», но это совсем не означает, что и на интервале оно наилучшее, что хорошо видно из графиков ошибок.

Впервые строгую постановку задачи приближения функции многочленом на интервале предложил П.Л.Чебышев:

«среди всех многочленов данной степени найти тот, который дает наименьшие абсолютные величины разностей значений функции и многочлена при всех значениях аргумента в данном интервале его изменения».

Понятно, что для симметричного интервала (-a,a) такой многочлен нулевой степени - это нуль, а многочлен первой степени уже вовсе не x. Какой же это многочлен для (-a,a)? А для (0,a)? Такие вопросы можно ставить как темы проектных работ.

Нечисловые задачи оптимизации.

Задача «распутывания», решаемая в первом занятии, послужила основой для ряда аналогичных задач, не имеющих прямого числового критерия оптимальности. Тем не менее эти задачи традиционно относятся к курсу «экстремальные задачи». Заметим, что ни классификацию задач, ни методы их решения мы в курсе не затрагиваем. Более того, рассматривать ли теоретические результаты, прямо относящиеся к решаемой задаче, решать учителю в зависимости от ситуации в классе. Например, если учащиеся вышли на проблему планарности графов эмпирически, то есть построили такие фигуры, которые «распутать» оказалось невозможно - то они готовы к восприятию соответствующего теоретического результата - теоремы Понтрягина-Куратовского о планарности графов (доказательство можно предложить разобрать желающим).

Постановка задачи.

Построить связный граф с самопересечениями так, чтобы при перемещении вершин за некоторое число шагов (от 3 до 10) можно было бы перейти к графу без самопересечений (На плоскости он называется «планарный граф»).

Ход построения модели.

Несколько свободных точек соединяется отрезками. Затем точки передвигаются, а отрезки между ними стираются или создаются с целью добиться нужных качеств модели. Задача не должна иметь очевидного решения, но не должна быть и чрезмерно сложной; решений должно быть много, но оптимальных решений - одно или несколько (немного).

Задача может осложняться геометрическими ограничениями - например, некоторые отрезки могут иметь фиксированную длину, некоторые точки могут двигаться только по заданной траектории и т.п.

Методика проведения занятия.

Учащиеся создают задачи-модели, подписывают их и пытаются решить задачу сами. Свои решения они запоминают в отдельном файле.

Первая пара учащихся, создавших модели-задачи с файлами ответов, обмениваются задачами и взаимно фиксируют время и качество решения.

Затем процесс взаимного решения строится как турнир, по выбираемой преподавателем схеме (турнирной таблице).

Второй турнир готовится и проходит с усложненными задачами (с ограниченными возможностями перемещения вершин графа).

Фигура, подготовленная Многоугольник, построенный одним из учеников в рамках состязания по быстрому распутыванию. на занятиях в СУНЦ (2003-2004г.г.). Денис Терентьев (i - школа) распутал эту фигуру за три движения вершин.

Пояснение. Это фигура, состоящая из свободных точек, соединенных отрезками. Точки свободны, поэтому их можно мышкой перемещать в любом направлении на любое расстояние. Отрезки при таком движении соответственно меняются, оставаясь привязанными к тем же точкам. Изменяется геометрия фигуры - пересекающиеся отрезки могут стать непересекающимися и наоборот.

Задача, которая ставится при работе с готовой фигурой - «расправить» ее так, чтобы исчезли все пересечения отрезков. Не каждую фигуру можно так расправить. Но данную фигуру расправить можно. Более того, ученик Школы дистанционной поддержки Денис Терентьев распутал ее за три движения мышкой. На втором рисунке показана уже расправленная фигура.

Первая задача, поставленная на занятии по построению подобных фигур, такова:

1) Задача «расправления» для данной фигуры должна иметь решение.

2) Количество звеньев в ней - от 15-ти до 20-ти.

3) Сложность распутывания должна быть максимальной.

После построения проводились состязания - построившие фигуру соседи менялись местами, и пытались распутать фигуру друг у друга. В паре побеждает тот, кто скорее распутает. Можно провести небольшой турнир, схема которого

выбирается в зависимости от имеющегося времени и состава класса. Победители могут определяться по двум критериям - кто быстрее всех распутывает, и чья фигура оказалась самой сложной для распутывания (при примерно равном количестве звеньев).

Эта работа дает ощущение границ планарности графа, поскольку обязательное требование - сначала распутать свою фигуру самому, и при построении учащиеся вынуждены обходить эти границы, то есть подбирать планарный граф. В этом случае упомянутые границы легко поддаются точной математической формулировке, согласно теореме Понтрягина-Куратовского.

Вторая задача, поставленная на занятии по этой теме, содержит элементы оптимизации, и формулируется так:

1) Задача расправления должна иметь несколько решений.

2) Эти решения существенно различаются по количеству шагов (шагом считается одно перетаскивание мышкой вершины).

3) Количество вершин и звеньев небольшое - 10-20.

4) Автор задачи подготовил хотя бы одно удачное (не обязательно оптимальное) решение своей задачи.

Эта задача по постановке существенно отличается от первоначальной. Скорость здесь не является критерием качества решения, возможно даже, наоборот. Она довольно близка известным головоломкам, например, головоломкам на зачеркивание заданной конфигурации точек непрерывной ломаной из заданного (или наименьшего) числа звеньев.

Такие задачи можно дать на дом - для желающих, с тем, чтобы ими обменяться. Решать их, конечно, тоже нужно не на занятии - на занятии можно только делиться лучшими задачами и решениями и обсуждать (а возможно, и доказывать) их оптимальность.

Третья задача, ставившаяся на занятиях по этой теме, является усложнением первой или второй.

Разница в том, что конструкция фигуры принципиально меняется - она может состоять не только из свободных точек, но и из связанных какими-то ограничениями. Например, какие-то из точек расположены на общей окружности, которая спрятана (не видна) и т.п. Но сложность задачи распутывания для таких фигур становится трудно предсказуемой, поэтому сразу нужно ограничиться небольшим количеством звеньев.

Эта постановка смыкается с постановкой типа «черные ящики», (см.2) так как при распутывании нужно учитывать неизвестную вначале внутреннюю структуру фигуры.

Опорные теоретические результаты.

Главным теоретическим результатом здесь служит теорема Понтрягина-Куратовского о планарности графа.

Граф планарен тогда и только тогда, когда он не содержит среди своих подграфов K(3,3) и К(5) (двудольного графа 3-3 и полного графа с 5-ю вершинами).

При желании можно рассказать о других критериях и об алгоритмах укладки графов. Можно отметить привязанность критерия к плоскости - на торе, например, К(3,3) укладыватся.

Задачи на ручное моделирование.

К задачам на нечисловую оптимизацию можно отнести и задачи на ручное построение, непосредственно примыкающие к задачам на распутывание.

Мы использовали для этого задачи на построение правильных звезд, пяти- , семи- и девятиугольной звезды.

Задание имело две части - компьютерную и «бумажную».

Несмотря на симметрию, облегчающую рисование такой звезды, соответствующий навык рисования (а это тоже - моделирование, и даже математическое) на бумаге у большинства учащихся есть только для пятиугольный звезд. Сколько-нибудь симметричную семиугольную звезду на бумаге мало кому удается нарисовать с первого и даже с пятого раза, не говоря о девятиугольной.

Тем не менее, есть два простых правила, зная которые, нетрудно сделать процесс ручного рисования звезды сходящимся к верному изображению.

Первое - нужно представить себе вписанную в звезду окружность, и стараться проводить ломаную так, чтобы звенья были касательными к ней.

второе - критерием правильности нарисованной звезды может служить наличие правильного (или хотя бы неправильного) семиугольника внутри нее.

В компьютерном варианте начертательные возможности увеличиваются, но соответственно растут и требования к результату.

Мы строим пятизвенную (затем семи- или девятизвенную) замкнутую ломаную, и «расправляем» ее до правильной звезды.

Этот вариант мало бы отличался от «бумажного», если бы не было возможности автоматизированного оценивания результатов работы.

Здесь мы применяем новый методический прием, специфичный именно для динамических моделей.

Дело в том, что динамическое разворачивание работы с чертежом дает возможность нетекстового (невербального) методического сопровождения процесса обучения. Эта идея восходит еще к работам И.В.Роберт (?) и А.А.Кузнецова (?) о неэффективности для компьютерных обучающих программ одной текстовой (включая рисунки) форме.

Для геометрических задач такое синхронное и естественное сопровождение процесса работы строится особенно просто. Нужно только подобрать дополнительные построения такого вида, что они включаются в процесс работы учащегося с задачей в заданный момент.

Не обязательно их при этом даже прятать эти построения - достаточно подобрать их так, чтобы они «работали» подсказками или указателями

только на некотором этапе работы.

Для нашей задачи таких построений можно предложить несколько.

Три этапа решения манипулятивной задачи - сдвигая мышкой вершины многоугольника, перевести его в пятиугольную звезду.

Пояснение. Серединные перпендикуляры к звеньям ломаной - это дополнительные построения, подобранные так, что они «работают» подсказками или указателями только на некотором этапе решения. Видно, что на первом этапе (рисунок 1) они не помогают решить задачу. На втором этапе (рисунок 2) они уже дают некоторую ориентацию. На третьем, заключительном этапе (рисунок 3) они дают критерий точности решения - и нужно добиться полного совпадения нужных точек.

Первое, самое простое построение - серединные перпендикуляры к звеньям ломаной.

Чтобы прямые, или лучи-перпендикуляры не загромождали чертеж при работе, их можно «укоротить», заменив на отрезки некоторой длины.

Длину удобно взять переменной, например, пропорциональной длине соответствующего звена ломаной. Можно взять и другую величину, например, пропорциональную средней длине всех звеньев. Коэффициент пропорциональности подбирается так, что при окончательной форме ломаной, то есть при форме звезды, отрезки на серединных перпендикулярах сходились точно в ее центре.

При хаотичном расположении звеньев дополнительные построения так же хаотично выглядят, и не являются подсказкой на этом этапе работы.

Только когда ломаная приобретает форму, близкую к форме правильной звезды, «геометрическая подсказка» начинает «работать», помогая уточнить форму, трудно поддающуюся уточнению «на глаз», даже при использовании другой подсказки - окружности, на которой можно расположить вершины звезды.

Дополнительная подсказка к решению манипулятивной задачи - окружность, начерченная «около» многоугольника.

Пояснение. На этом, заключительном этапе работы, подсказка помогает повысить точность решения - но автоматически полного совпадения нужных точек она не дает, так как она подсказывает только равенство расстояний, а не углов. Приходится уточнять положения вершин на окружности вручную, пользуясь «встроенной» подсказкой - вписанным пятиугольником.

Другое построение, «работающее» на более поздней стадии построения, таково:

строим звезду, гомотетичную данной, с коэффициентом гомотетии, подобранным так, чтобы при окончательной форме ломаной эта «малая» звезда оказалась вписана внутри «большой».

Встроенная подсказка другого вида - гомотетичный многоугольник специально подобранного масштаба. Задача та же - начертить из данных ломаных правильную звезду.

Пояснение. Многоугольник вокруг центральной точки - это дополнительное построение, подобранное так, что оно «работает» подсказкой или указателем только на некотором этапе решения. Видно, что ни на первом (рисунок 1), ни на втором этапе (рисунок 2) они не помогают решить задачу.

Можно подобрать и другие построения в соответствии с общим принципом - подсказка не мешает на стадии, где она не помогает, и указывает путь решения на запланированном этапе работы.

Значение манипулятивной работы с моделями раздела.

Этот раздел заданий в теоретическом отношении носит пропедевтический характер. Но этого нельзя сказать о практическом значении заданий, так как ручная работа даже с простейшими фигурами и простейшими заданиями на их модификацию у большинства учащихся (и даже у учителей) встречает значительные трудности. И эти трудности отнюдь не связаны с компьютерным характером работы. Некоторые задания, включенные в раздел, выполняются карандашом на листе нелинованой бумаги - и наш многолетний педагогический опыт показывает, что и они вызывают те же сложности.

О типичных трудностях ручного геометрического моделирования.

Приведем простой пример: построение пяти-семи-девяти-угольных звезд. Пятиугольные звезды многие школьники (но не все) умеют рисовать с детства. Тем не менее переместить вершины замкнутой ломаной так, чтобы получилась пятиугольная звезда, получается у многих далеко не сразу!

Задача на рисование семиугольной звезды (в центре - геометрическая подсказка, которая точно впишется в звезду при правильном решении)

Пояснение. Нужно, двигая мышкой вершины (вершины маленького многоугольника мышкой «не зацепляются»), получить правильную семиугольную звезду. Кнопки 1-2 дают «слабую» подсказку - окружность (на рисунке она показана), кнопки 3-4 показывают\прячут одно из решений.

Второй пример - безкомпьютерный. Задание хотя бы очень приближенно нарисовать семиугольную звезду встречает большие трудности почти у всех учащихся (и у многих чителей), а тем более - девятиугольную! Хотя после небольшой тренировки (и здесь компьютер многим школьникам помогает понять логику построения) почти все приобретают этот навык. Если есть геоплан - еще лучше! С этим инструментом достигается более глубокое понимание задачи.

Это задание - одно из тех, где ясно видно, что компьютерное и натурное моделирование должны дополнять друг друга, и как важно выстроить их взаимодействие и взаимодополнение на занятиях.

Стереометрия

Построение вращающейся модели вписанного в куб икосаэдра и ромбооктаэдра.

Истоки задачи.

Это задание вдохновлено чертежом В.Н.Дубровского. Им разработана новая методика решения стереометрических задач, существенно использующая возможность вращения фигур и построений на проекциях, легко и естественно выполняемых в средах типа «Живой Геометрии». (ссылка на Дубровский, ИНТ 2005)

Таким образом, компьютерные инструменты не только расширяют возможности традиционного курса математики. Они уже сегодня дают новые, привлекательные и мощные методы поиска, исследования и решения геометрических и стереометрических задач, в том числе и вполне традиционных по постановке.

Этапы работы над моделью куба.

Работа над моделью также состоит из нескольких этапов, и каждый этап может быть реализован с различным уровнем сложности.

Упрощенный вариант моделирования.

Самые простые варианты моделирования куба - построения

по четырем точкам
переносом квадрата
из моделей параллелограммов

Эти модели не являются на своих областях определения наглядными и удобными проекциями. Лишь при небольших перемещениях они создают иллюзию объема, позволяя решать простейшие задачи. Но их преимущество - в простоте и в скорости построения.

Модель куба по четырем точкам и модель куба через сдвиг квадрата.

Пояснение. На первом рисунке достраиваются (путем параллельного переноса) вершины проекции, задаваемой четырьмя свободными точками.

На втором рисунке построен квадрат, вектор переноса этого квадрата, и результат переноса. Соединив вершины квадратов, получим простейшую проекцию квадрата, на которой он выглядит объемным.

На этих чертежах можно получить параллельную проекцию куба на плоскость, но при этом придется подбирать положение одной из точек, так как это модель не куба, а, в лучшем случае, прямоугольного параллелепипеда, у которого одна сторона - квадрат..

Поэтому поворачивать ее также или на небольшой угол, или придется корректировать неточности поворота, подтягивая другие остальные точки (кроме той, за которую вращаешь).

Модель куба из параллелограммов: строим инструмент «параллелограмм», и им строим модель. На этих двух рисунках представлены этапы получения еще одной простейшей модели куба.

Пояснение. На первом строится инструмент «параллелограмм», на втором показано, как с помощью этого инструмента строится модель. От первой модели она отличается только выбором исходных точек - он более гибкий за счет двухуровневой схемы построения модели (первый уровень -инструмент, второй - уже сама модель).

Все эти модели подходят для дальнейших этапов, но дополнительные задачи на них выполнять или сложно, или невозможно. Потому, например, что модель из параллелограммов далеко не всегда является проекцией куба, а на модели «сдвинутый квадрат» моделируется поворот (небольшой) только вокруг «вертикальной» оси.

Базовая модель куба.

Следующий по трудоемкости построения вариант - модели с вращением (на 90 градусов или больше). одна - с вращением по одной оси, другая - с вращением по двум осям. Обе эти модели опишем одновременно, так как по построению и управлению они отличаются немногим.

Итак, выделим и опишем следующие этапы работы над моделью куба.

Построение модели вращающегося квадрата.
Построение модели вращающейся пирамиды.
Построение сечений на вращающейся пирамиде.
Построение модели куба. Сечения куба и другие задачи.
Построение инструмента «отрезок внутри отрезка» с параметром.
Построение параметрической модели многогранника на базе куба, превращающегося в усеченный куб, икосаэдр и ромбододекаэдр.

Построение модели вращающегося квадрата.

Поскольку точное обоснование математической модели относится к предмету «математика», на занятии по информатике мы, как обычно, ограничимся «правдоподобными рассуждениями» (в духе Пойа []), правильными, но не доходящими до доказательства по уровню строгости.

Если мы смотрим на окружность «сверху», мы видим окружность. Ее прямая проекция на перпендикулярную ей плоскость также будет окружностью. Если мы смотрим на нее под углом, то ее проекцией будет эллипс, так как соответствующая проекция наклонной короче. Вначале выберем самый простой вариант проекции - когда по одной оси (ординат) наклонная такова, что все проекции отрезков на этой оси ровно вдвое меньше самих отрезков, а по другой оси - оси абсцисс - расстояния не меняются. Можно подобрать проекцию так, что не будут меняться они и по третьей оси.

Пояснение (чертеж-иллюстрация) к понятию модели объемной фигуры - как параллельная проекция на удобно расположенную плоскость может быть моделью пирамиды. Он используется не для изготовления на занятиях, а для просмотра на вводной части занятия по теме стереометрия. Иллюстрирует специфику параллельного проектирования.

Пояснение. При вращении этого чертежа важно дать увидеть, что одна пирамида - объемна, а другая является чертежом на плоскости, и также уяснить специфику параллельного проектирования. Для этого чертеж поворачивается, при этом может включаться/выключаться видимость необходимых для пояснений параллельных линий и параллельных плоскостей.

Это значит, что для построения проекции точки на окружности достаточно эту точку на окружности заменить точкой, расстояние которой от некоторой оси проектирования будет в два раза меньше (или, для модели с переменным наклоном, в некоторое - переменное - количество раз меньше).

Ось также выберем самую простую - горизонтальную прямую, проходящую через центр окружности.

Почему расстояние до оси проектирования уменьшается вдвое.

Чертеж-иллюстрация. Он используется не для изготовления на занятиях, а для просмотра на вводной части занятия по теме стереометрия. Иллюстрирует специфику параллельного проектирования.

Пояснение. Чертеж является упрощенной частью предыдущего чертежа. Он помогает ответить на вопрос, почему часть отрезков при изготовлении проекции уменьшается (например, вдвое), а другая часть - не изменяется в длине.

Если мы возьмем квадрат, вписанный в окружность (он полностью определяется одной точкой на окружности и самой окружностью), то его проекция будет строиться по четырем точкам вершин.

Строится проекция квадрата. На "линию горизонта" проектируются четыре вершины квадрата.

Пояснение. Вершины квадрата построены как концы перпендикулярных диаметров. При вращении вокруг центра они оставляют след - окружность. На рисунке видно, что точки, взятые как проекции этих вершин, оставляют при таком движении след - эллипс, то есть окружность при нашем проектировании перешла в эллипс, так как расстояния по вертикали сжимаются (у нас - в два раза).

Их можно соединить отрезками, которые и будут проекциями сторон (доказывать это мы тоже не будем, хотя стоит обратить внимание на необходимость доказательства).

Построение модели вращающейся пирамиды.

Пользуясь тем, что проекция по третьей оси не меняет расстояний, получим проекцию отрезка на перпендикуляре к окружности из ее центра.

Соединив полученную проекцию с проекциями вершин, получим модель пирамиды.

Строится проекция пирамиды. Четыре вершины проекции квадрата и точка вершины пирамиды соединяются отрезками.

Пояснение. Точка А - ведущая, она построена на окружности, и при ее движении вращаются вершины квадрата, вращается и проекция. Эту точку нужно оставить, остальные исходные пострения можно спрятать.

Двигая точку А мышкой, мы можем поворачивать проекцию. Вместе с проекцией будут поворачиваться все построения, исходные точки которых ей принадлежат.

Построение сечений на вращающейся пирамиде.

Построим на ребрах, исходящих из вершины пирамиды, четыре свободные точки. По ним построим многоугольник и закрасим его подходящим цветом.

Место для точек можно выбирать случайным образом, как вручную, так и автоматически. На уроке более целесообразно выбирать вручную. При необходимости рандомизации можно использовать команду мультипликация.

Вопрос: будет ли полученный многоугольник сечением данной пирамиды некоторой плоскостью?

Строится проекция пирамиды, и многоугольник по четырем точкам на ее наклонных ребрах. Будет ли полученный многоугольник сечением?

Поясненеие.

Двигая точку А мышкой, мы можем поворачивать проекцию. Вместе с проекцией будет поворачиваться и многоугольник. Если при повороте в какой-то момент он сожмется в отрезок, значит, четыре точки лежат в одной плоскости, и задают сечение.

На рисунке показано это вращение. Видно, что эти точки не задают сечения. При некотором угле поворота многоугольник превратился в невыпуклый, что невозможно для точек, задающих сечение. Но все же на этой модели невозможно всякое сечение превратить в отрезок подходящим вращением - из-за фиксированности угла наклона проекции в этой модели.

Ответить на этот вопрос, глядя на единственную проекцию, обычно непросто. Вращение модели сразу дает ответ!

Но наша модель вращается только в одной плоскости, и не для всех расположений четырех точек достаточно этого вращения.

Модификация модели несложна - вместо половины расстояния при построении проекции нужно брать переменную долю, для всех четырех точек одинаковую, и зависящую от параметра. При изменении параметра проекция будет поворачиваться уже в другой плоскости. Построенной так дополнительной возможности поворота уже достаточно для решения поставленной задачи.

Строится проекция пирамиды с переменным наклоном проекции, и многоугольник по четырем точкам на ее наклонных ребрах.

Пояснение. Двигая точку А мышкой, мы можем поворачивать проекцию. Вместе с проекцией будет поворачиваться и многоугольник. Если при повороте в какой-то момент он сожмется в отрезок, значит, четыре точки лежат в одной плоскости, и задают сечение. На рисунке показано это вращение. При некотором угле поворота многоугольник превратился в невыпуклый, что невозможно для точек, задающих сечение.

Опыт решения нескольких таких задач может подсказать идею доказательства. Но здесь мы снова вступаем на территорию предмета математики, и целесообразно оставить доказательство на факультатив по математике (или другую форму дополнительных занятий).

Четыре точки на одной прямой.

Можно доказать (опять же в курсе информатики мы этого делать не будем), что если эти четыре точки задают плоскость, то при вращении возникнет ситуация, когда все они будут на одной прямой, и не возникнет ситуации, когда многоугольник станет невыпуклым. Но это утверждение на вращающейся модели становится в буквальном смысле очевидным! Перебирая различные случайные конфигурации и корректируя их, двигая точки - «кандидаты в точки сечения» - учащиеся могут сами сформулировать эту и ей подобные теоремы, и догадаться о путях доказательства.

Поиск и решение в задаче о сечении.

На этой же модели естественно задать вопрос - а как получить четвертую точку, если три уже заданы (модель позволяет понять, что именно три точки определяют сечение). Так мы приходим к традиционной задаче построения точек сечения - от более гибкой модели к более жесткой, через «ручную» работу, «ручную» вариацию параметров.

Этот путь понимания представляется нам более прямым, так как задача (или теорема) появляются здесь не как ответы на еще не заданные вопросы, а как подсказка на пути самостоятельного поиска (в худшем случае), или как самостоятельное открытие - хотя и в рамках заданной модели.

О простоте задачи построения сечения на модели.

Все построения задачи поиска сечения на модели выполняются обычным образом, поскольку при нашем проектировании параллельные остаются параллельными и пересечения прямых остаются пересечениями прямых. Научить учащихся строить сечения нетрудно, и получающиеся вращающиеся модели довольно эффектны, особенно если дополнять их натуральными моделями (деревянными, пластмассовыми, картофельными и т.п.).

Построение модели куба. Сечения куба и другие задачи.

Построить модель куба можно, например, так. Если вспомнить, что расстояния по третьей оси тоже не меняются, и вершину пирамиды построить так, что ее высота будет равна стороне квадрата, а затем из нее провести параллельные проекциям диагоналей квадрата, то на их пересечениях с перпендикулярами из остальных вершин проекции квадрата и получим недостающие 4 вершины модели куба.

Все сказанное о модели пирамиды можно повторить и о модели куба. Приведем пример модели сечения, подготовленной учащимся 10-го класса СУНЦ.

Пример модели сечения (работа Андрея Румянцева, СУНЦ, 11-в, 2000 г.)

Пояснение. Работа по теме «сечения, включающая случайную анимацию по двум или трем точкам сечения одновременно, и доказательство правильности сечения путем подбора подходящего проектирования (поворот и наклон моделируются вручную).

Если выделить точку, определяющую квадрат, а затем образующую - ребро пирамиды, куба или грань куба или пирамиды - и применить команду «геометрическое место точек» - то мы получим модель поверхности вращения (или тела вращения) - цилиндр или конус.

Интересной задачей является построение поверхности вращения других отрезков прямых в модели - в частности, легко получаются гиперболоид вращения и усеченный конус.

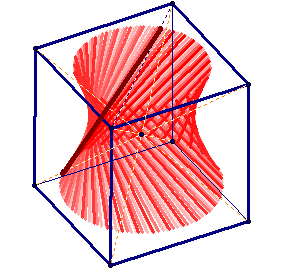
След вращения отрезка в кубе - гиперболоид вращения

Пояснение. При различных расположениях отрезка в кубе при вращении куба вокруг центральной оси отрезок образует гиперболоид вращения и т.д..

Построение инструмента «отрезок внутри отрезка» с параметром.

Это типичный вспомогательный инструмент для сложных моделей. Данный инструмент, несмотря на простоту, содержит все основные черты таких инструментов, включая геометрически заданный параметр.

Строится он так - задается параметр в виде двух свободных отрезков, считывается их отношение, и по этому отношению исходный отрезок делится точкой по команде «гомотетия». Затем к исходному отрезку строится серединный перпендикуляр, и относительно него отражается полученная точка.

По двум полученным точкам строится нужный отрезок, а по всей конструкции - инструмент. Сценарий инструмента модифицируется - имена отрезков-параметров (или их концов) объявляются «соответствующими объекту с тем же именем на чертеже», т.е. имена фиксируются.

Теперь любое множество отрезков можно заменить на их пропорциональные длине доли, да еще симметричные относительно середины отрезков.

Построение треугольника с помощью созданного инструмента "отрезок в отрезке".

Пояснение. Два отрезка вверху чертежа задают отношение, в котором отрезок подвергается гомотетии относительно своего центра. Исходный отрезок прячется, остаются только его концы (на рисунке он остался - пунктиром). Таким инструментом можно работать точно так же, как стандартным инструментом "отрезок", как это и видно из рисунка, где построенный треугольник двигается мышкой..

Построение параметрической модели многогранника, превращающегося в усеченный куб, икосаэдр и ромбододекаэдр.

Проведем на каждой грани куба отрезок посередине, соблюдая симметрию, указанную на чертеже. Зададим параметр - нанесем два свободных отрезка на чертеж с именами, зафиксированными в инструменте «отрезок в отрезке». Теперь заменим каждый отрезок на грани с помощью инструмента, и соединим концы новых отрезков.

Параметр нам нужно менять в таких пределах, чтобы фигура изменялась от усеченного куба до от ромбододекаэдра. При некотором промежуточном значении параметра (при равенстве всех ребер фигуры) мы получим икосаэдр.

Итоговый чертеж: три положения параметра - три знакомые фигуры.

В качестве домашнего задания (для тех, кто себе сам его не придумал) можно предложить этот же прием повторить на октаэдре и тетраэдре, взяв отрезки не на гранях, а на ребрах.

Пример решения задачи для октаэдра.

Задача из Г.Фройденталя

Постановка задачи - куб наизнанку.

В книге замечательного математика-педагога Ганса Фройденталя (Фройденталь Г. Математика как педагогическая задача в 2 томах. М. Просвещение 1982-1983г.) предлагается представить себе, какая фигура получится, если куб, разрезанный на пирамиды по линиям, соединяющим вершины с центром, «вывернуть наизнанку».

Как «вывернуть куб наизнанку», используя его симметрию.

Модель вращающегося куба очень удобна для решения этой задачи, так как дает ту визуализацию поворотов, которой не хватает, чтобы уяснить форму получающейся фигуры.

Два решения - лобовое и с использованием симметрии.

Задача полезна не только тем, что иллюстрирует важные стереометрические понятия из теории многогранников.

Она допускает по крайней мере два простых пути решения.

Первое решение - лобовое. На каждой грани строим пирамиду, симметричную соответствующей внутренней относительно этой грани.

Второе решение основывается на идее замены отражения пирамиды переносом. Если заметить, что отраженная пирамида уже готова - а именно, она симметрична данной относительно центра куба - то построение будет состоять в сдвиге куба в шести направлениях, задаваемых его ребрами.

Заметим, что этот чертеж сразу дает и очевидное доказательство того, что грани новой фигуры - ромбы. Для этого достаточно обратить внимание на плоскости, разрезающие кубы через противоположные (симметричные относительно центра) ребра.

Результат трех таких сдвигов (из шести) показан на чертеже.

Теперь остается только спрятать невидимые линии, раскрасить грани полученной фигуры и повращать ее для уяснения ее формы.

Этапы получения фигуры «куба наизнанку»

Возможное развитие задачи.

Описанная конструкция дает возможность учащимся самостоятельно строить трехмерные графики и т.п.

В проектных работах на эту тему можно использовать материалы, поясняющие построение таких конструкций, и выложенные на сайте создателей среды (http://www.keypress.com).

Пример модели с трехмерным динамическим графиком из стандартной поставки Geometer's SketchPad v.4.

Литература:

А.А. Кузнецов, Л.О. Филатова Информатика в профильной школе // Информатика и образование.- 2003.- N 6.- C. 14-18.
Роберт И. В. Современные информационные технологии в образовании: дидактические проблемы; перспективы использования. // М., 1994.
Белошапка В.К. Информационное моделирование в примерах и задачах.//- Омск: Из-во ОГПИ, 1992.
Цукарь, А.Я. Дидактические материалы по геометрии с элементами исследования для 7 класса // М.: Просвещение, 1998. - 79 с.
С. Бешенков, Е. Ракитина, Моделирование и формализация. Методическое пособие // М.:ЛБЗ,2002,-336 стр.
Шабат Г.Б. О компьютерном эксперименте в преподавании математики // "Монитор-Аспект", 1995, 6. - с.122-125.
В.Н. Дубровский, А.В.Земляков, А.В.Пантуев, А.В.Чехлова и др., Образовательный комплекс"Математика, 5-11 классы. Практикум", ЗАО"1С", 2003.
В.Н. Дубровский “Практикум - новая форма электронного образовательного издания по математике”// сб.докладов Международной конференции ИТО-2003. М: РУДН, 2003, с.65-69.
В.Н. Дубровский “СТЕРЕОМЕТРИЯ С КОМПЬЮТЕРОМ // Компьютерные инструменты в образовании. - СПб.: Изд-во ЦПО "Информатизация образования", 2003, №6, С. 15-23.
А.В. Пантуев “Виртуальные лаборатории и активизация работы школьников” // сб. “Стимулирование познавательной деятельности студентов и школьников”, М: МГПУ, 2002, с. 30-33.
Фалина И.Н., Андреева Е.В, Математические основы информатики. Элективный курс. //Элективные курсы в профильном обучении: образовательная область “Математика”/Министерство образования РФ - Национальный фонд подготовки кадров. -М.,Вита-Пресс, 2004 (http://www.profile-edu.ru/files/1_04_04/Matematika.pdf)
Выготский Л.С. Орудие и знак в развитии ребенка // Собр. соч. Т. 6. М.: Педагогика, 1984.
Поздняков С.Н. Геометрия в движении (с компьютерной поддержкой). СПб.: ЦПО "Информатизация образования", 1995.
Храповицкий И.С. Эвристический полигон для геометрии // Компьютерные инструменты в образовании, 2003, 1.
Иванов С.Г., Поздняков С.Н. Компьютер в продуктивном обучении математике. "Комьютерные инструменты в образовании" 5, 2003 г.
Вопросы психологии учебной деятельности младших подростков. / Под ред. Д. Б. Эльконина, В. В. Давыдова. - М.: Изд-во АПН РСФСР, 1962. - 287 с.
Гальперин П. Я. Психология мышления и учение о поэтапном формировании умственных действий // Исследования мышления в советской психологии / Отв. ред. Е. В. Шорхова. - М., 1966. - С. 236-277.
Пантуев А.В. "Классификация средств интегрированной среды "Живая Геометрия" по типу занятия", сб."Дни науки МГПУ-2001 г." , МГПУ,2001 г.183 с., стр.105-107.
Давыдов В.В. Теория развивающего обучения. - М., 1996.
Беспалько В.П. Слагаемые педагогической технологии. - М., 1989.
Пойя Д. Математическое открытие. - М.: Наука - 1976.
Амонашвили Ш.А. Личностно-гуманная основа педагогического процесса. - Минск, 1990.
Шаталов В.Ф. Куда и как исчезли тройки. - М.: Просвещение, 1990.
Соловейчик С.Л. Педагогика для всех. М., 2000.
Эльконин Д.Б. Психология игры, М., 1978 г.
Шаталов В.Ф. Опорные конспекты по кинематике и динамике. - М.: Просвещение, 1989.
Библер В.С. Мышление как творчество. - М., 1975.
Гусев В. Геометрия. - М.: Авангард, 1996.
Давыдов В.В. Теория развивающего обучения. - М., 1986.
Потоцкий М.В. О педагогических основах обучения математики, М., 1963ъ
В.А.Успенский Семь размышлений на темы философии математики, в сб. «Закономерности развития современной математики», М.,Наука, 1988
В.П. Зинченко Психологические основы педагогики М.: Гардарики, 2002).
Талызина Н. Ф Педагогическая психология:.М.,«Академия»,2001
Лапчик М.П.,Семакин И.Г., Хеннер Е.К. Методика преподавания информатики, М., «Akademia», 2003. - 624 с.
Юдина А.Г. Практикум по информатике в среде «LogoWriter»: учебное пособие для общеобразовательной школы. - М.,ИНТ, 1997.
"Роботландия 96", пособие для учителя - Роботландия, Переславль-Залесский, 1996

Ландо С.К., Семенов А.Л. Учебная программа «Алгоритмика»:5-7 классы, - М., ИНТ, 1997.

Кушниренко А.Г., Лебедев Г.В. 12 лекций о том, для чего нужен школьный курс информатики и как его преподавать. : Методическое пособие .- М.: Лаборатория базовых знаний, 2000 (Вологда: Полиграфист, ПФ).- 464

Семакин И.Г., Шеина Т.Ю. Преподавание базового курса информатики в средней школе : Методическое пособие . - Лаборатория базовых знаний , 2002

Челак Е.Н., Конопатова Н.К. Развивающая информатика : Методическое пособие . - Лаборатория базовых знаний , 2001

Table of Contents

Экспериментальная оценка порядка приближения в точке.

О смысле параметра «порядок точности».

Организация работы по оценке порядка точности приближения в нуле.

Ограниченность полученного результата и темы проектных работ.

Нечисловые задачи оптимизации.

Постановка задачи.

Ход построения модели.

Методика проведения занятия.

Опорные теоретические результаты.

Задачи на ручное моделирование.

Значение манипулятивной работы с моделями раздела.

О типичных трудностях ручного геометрического моделирования.

Стереометрия

Истоки задачи.

Этапы работы над моделью куба.

Упрощенный вариант моделирования.

Базовая модель куба.

Построение сечений на вращающейся пирамиде.

Четыре точки на одной прямой.

Поиск и решение в задаче о сечении.

О простоте задачи построения сечения на модели.

Построение модели куба. Сечения куба и другие задачи.

Построение инструмента «отрезок внутри отрезка» с параметром.

Построение параметрической модели многогранника, превращающегося в усеченный куб, икосаэдр и ромбододекаэдр.

Задача из Г.Фройденталя

Постановка задачи - куб наизнанку.

Два решения - лобовое и с использованием симметрии.

Возможное развитие задачи.